quantified harmolodics

harmolodics is an approach to musical organization introduced by composer and multi-instrumentalist Ornette Coleman. Coleman found that when musical voices interact freely—like people—the sum of their interactions turns out to be perfectly intelligible. Quantified Harmolodics accounts for this intelligibility, starting from a radical premise: that every note is a key center unto itself, and every voice modulates according to its own an internal compass. It treats pitches like keys and intervals like modulations, in the understanding that it is the freedom to modulate that determines the horizon of harmonic intuition, while tonal procedures are essentially intramural to key and can always be collapsed to a point.

In this light, the operational domain of a voice is not determined by prior or surrounding operations, and this voice's relationship to other voices is always salient, no matter what it does and no matter what happens to it. Harmolodics can therefore register any contingency, and license any response. This offers a vital alternative to the incorrigible quest for compositional injunction. Because it concerns the combination of notes and voices, this quest incurs a fundamental price: inevitably, to give to one voice is to take from another. Every decision made for a given voice burdens its conspecifics, as well as its own horizon, with the recuperation or completion of some master protocol that looms over the concrete musical event like an obsessional symptom.

In contrast, harmolodics equates individuation and modulation, and takes the universe of relationships that emerge between voices as its domain (rather than the voices themselves, which remain unmolested). This domain arises in the discrete vector space generated by the modular arithmetic of modulation, and does not solicit the external authority offered by spectral objects, tone rows, contrapuntal rules, or other references. Null modulation is distinguished from absolute pitch, which appears tangentially as a residue of harmolodic algebra.

In lieu of procedures or conditions, harmolodics identifies the degrees of freedom available to voices. Coleman spoke of meeting a fellow traveler early in his career who was diligently formalizing this domain:

I met Buckminster Fuller in 1954, at Hollywood High in Hollywood California. When he demonstrated the way his domes are put together, and how geometric they were done, it just blew me away, because I said, “this is how I've been writing music. This is the way I write music.” And to me he became one of my—he's probably my best hero.

Fuller's “geometry of thinking” furnishes a parsimonious view of the musical paths illuminated in Coleman's insight. It unifies the gamut of intervallic functions and the proportions that open up between them in a format which is cardinal, isotropic, and linear, making the aggregate available to intuition in real time without specifying relative prominence or value.

Degrees of Modulation

Our ability to perceive frequency ratios distinguishes pitch as a discrete space, in contrast to other musical characteristics such as loudness (a one-dimensional continuum) or timbre (presumably some higher-dimensional manifold). Ratios striate the frequency continuum with thresholds, and while the difference between frequencies can vary continuously, pitches exhibit discrete difference insofar as they inhabit coordinates within these thresholds.

In the harmolodic orientation, the pitch classes generated by factors of two (octaves) correspond to keys, and the interval classes generated by factors of three (fifths and fourths) correspond to twelve degrees of modulation between these keys. The pythagorean comma and the commas separating these frequencies from those of higher prime factors do not produce new keys. Rather, these micro-intervals are experienced at a different scale of magnitude: the furrows around each pitch that underlie the phenomenology of intonation.

The space of modulation is captured in modulo 12 integer arithmetic—discrete ‘clock arithmetic’ In algebraic terms, it forms a cyclic abelian group of order 12. This means that 1) twelve degrees of modulation can be generated by repeatedly concatenating a single unit value; 2) any sequence of modulations produces an overall modulation which is also an element within the group; 3) a sequence of modulations can be shuffled, and subsequences can be merged into their local result, without changing its overall modulation; 4) there is a null modulation that doesn't move to a new key in the first place, and doesn't affect another modulation when concatenated to it; and 5) every degree of modulation has an inverse: a counterpart that brings you back to where you started.

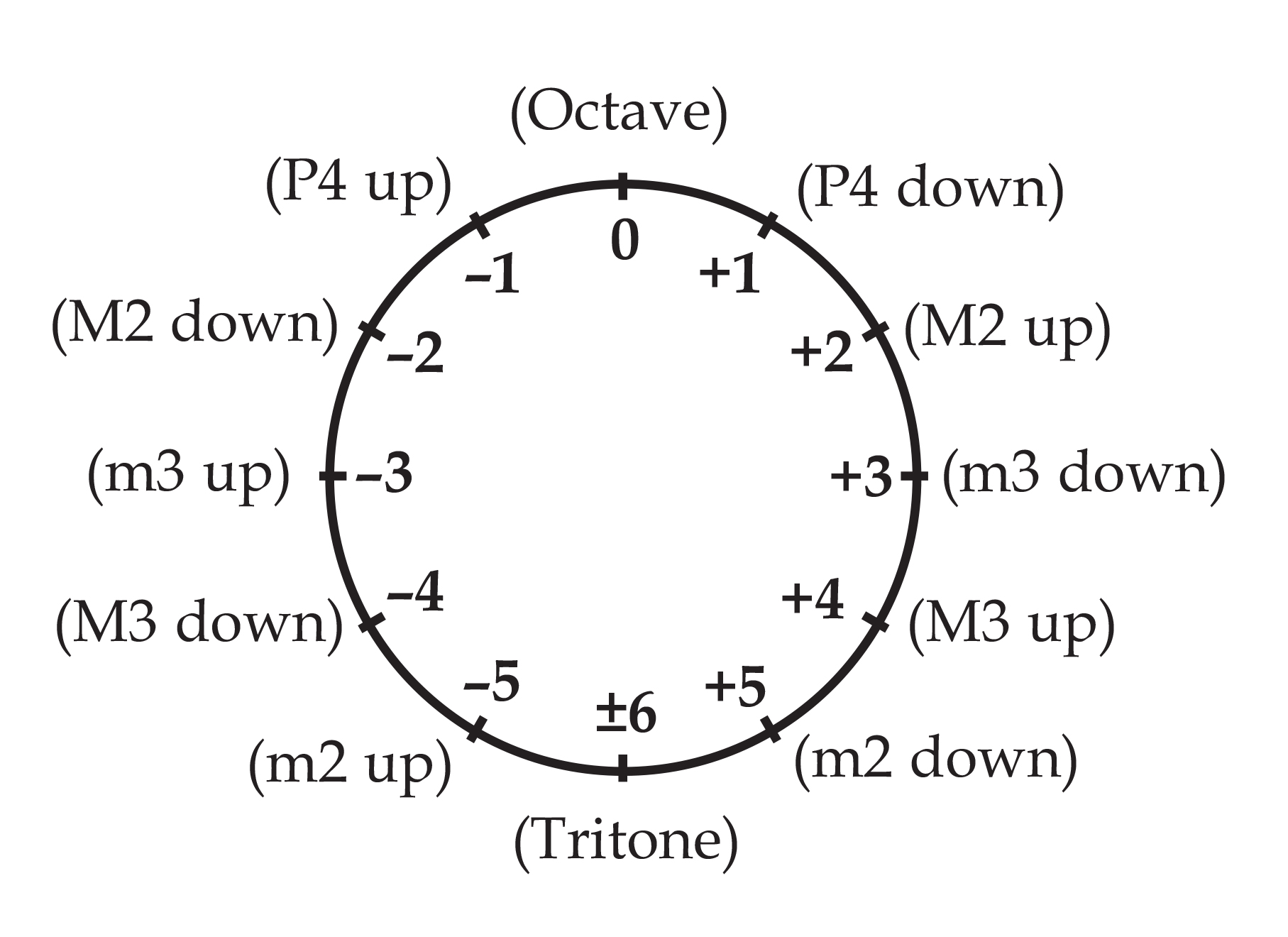
Our unit value corresponds to the interval class of a perfect fifth. As noted above, this interval class is found when frequencies are related by a factor of three—it represents the simplest harmonic relation after octaves, which correspond to null modulation. Perfect fourths correspond to the inverse, -1, since they nullify the effect of modulation by a fifth. However, the group contains another unit as well: because 5 is coprime with 12 (ie., it does not divide into 12), the corresponding modulation is also sufficient to generate and measure every other. Taking every fifth value in our ring, we arrive at an alternate ordering:

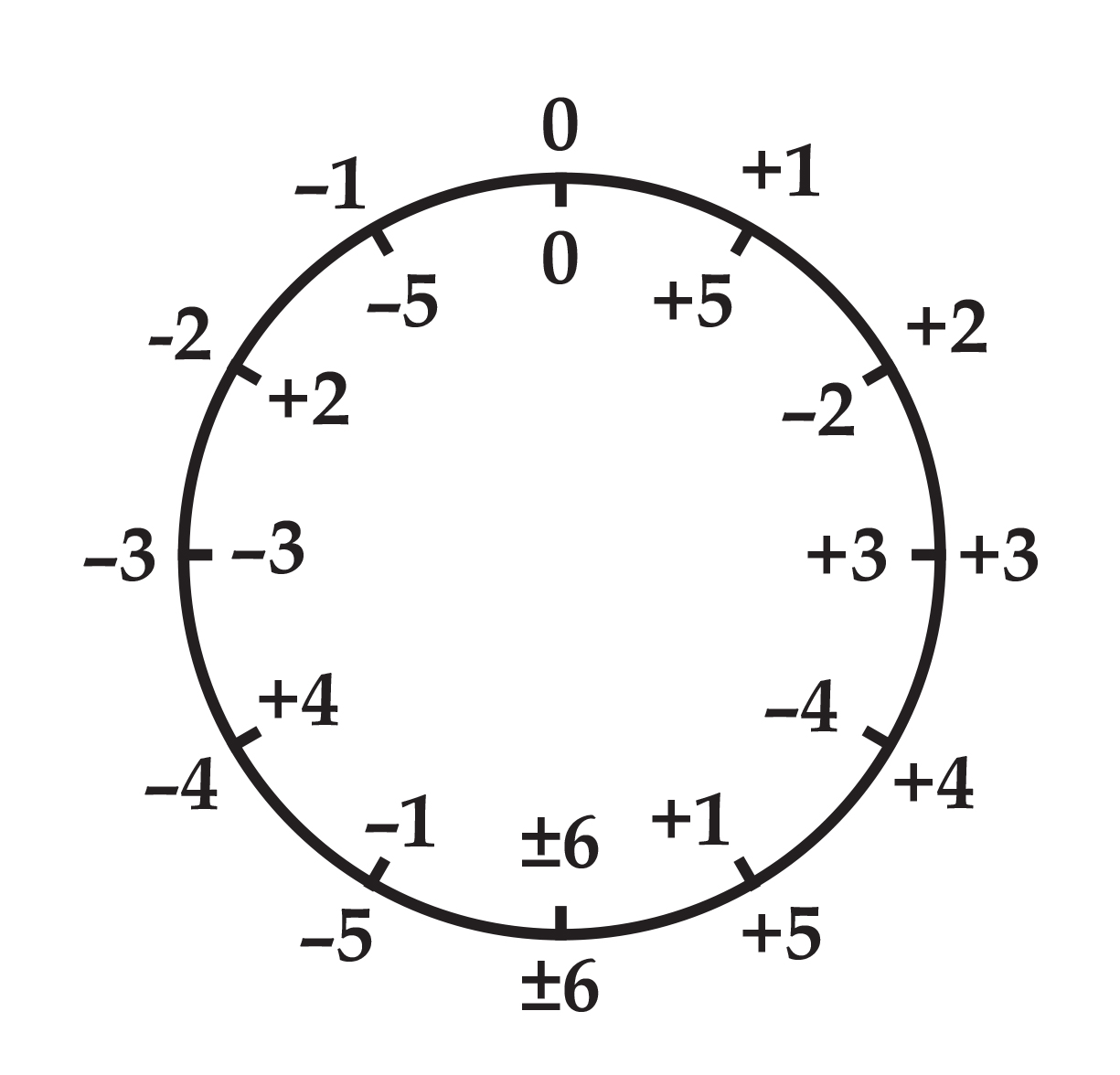
Degree |5| corresponds to half-steps. If +1 and -1 are ‘harmonic’ units that modulate to neighboring keys, +5 and -5 are ‘gradient’ units that modulate to those keys closest in frequency. Each type of unit is equal to five of the other: the smallest harmonic increment is equal to five gradient increments, and the smallest gradient increment is equal to five harmonic increments.

Degrees |4| and |3| correspond to thirds and sixths, which intersect frequency relationships that include factors and divisors of five. They provide modulation within the continuum of relative majors and minors. Unlike 1 and 5, they do not generate every other interval when iterated: they generate subgroups of order 3 and 4 respectively, corresponding to augmented chord intervals and diminished chord intervals.

Degree |6| modulates to the most distant key and is its own inverse (the most distant key from the most distant key is one's starting point). It generates a subgroup of order 2, corresponding to the tritone, which pairs a key with its antipode.

Degree |2| unifies the stepwise effects of the two unitary degrees: it is equal to two |5|s as well as two |1|s, and it can produce incremental gradient modulation (a difference in frequency which sounds like a ‘step') and incremental harmonic modulation at the same time. It generates a subgroup of order 6, corresponding to the whole-tone intervals, which evacuates the harmonic bonds found in degree |1| while preserving a sense of incremental measurement.

The dualism of unit modulation, and the reduced cardinalities generated by the other degrees of modulation, reverberate in every elaboration of harmolodic structure.

The Gamut of Proportions

Three pitches coincide three degrees of modulation (that is, undirected modulations) and three minimum curves (undirected changes in modulation). There are thirty-one of these triplicities of pitch, modulation, and curvature. Twelve incorporate null modulation, duplicating a key, a degree of modulation, and a curve:

Five exhibit null curvature, duplicating a degree of modulation:

There remain 14 non-redundant proportions, which can be grouped in 7 inverse pairs:

Any two non-redundant proportions share at least one degree of modulation, and so can be derived from one another by the replacement of a single key. In seven instances, proportions share two out of three modulations, as represented in the following diagram:

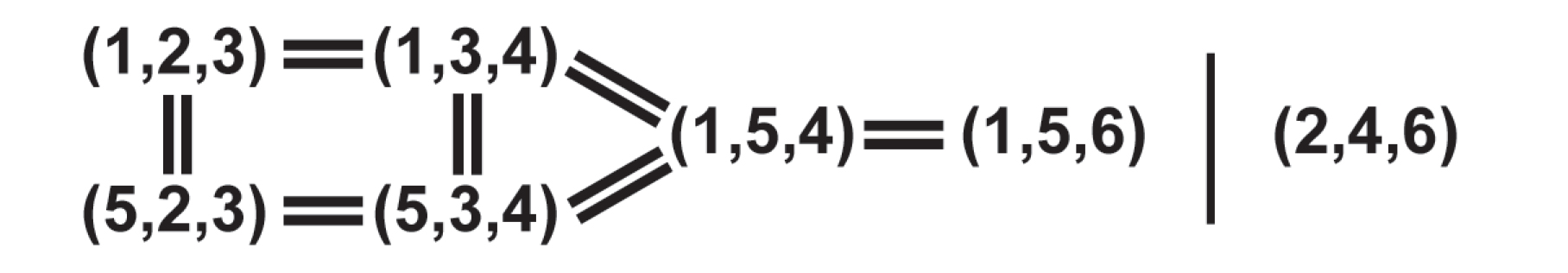
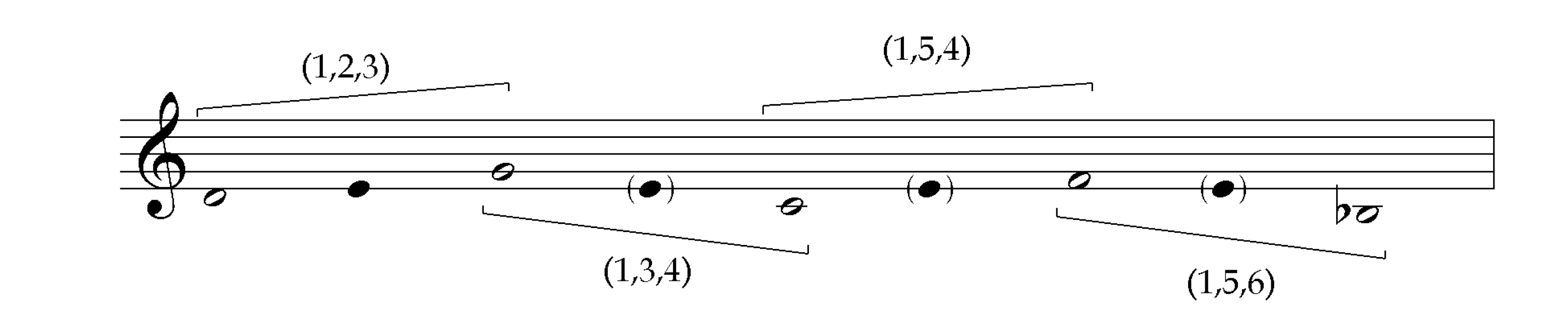
We can illustrate the relationship of these neighboring proportions by repeatedly transposing a representative trichord by one of its constituent intervals. The latter then establishes a series of intervallic frames:

A single interpolated note completes the proportion in each frame. These interpolated notes are themselves separated by the same interval, and frame the inverse proportion.

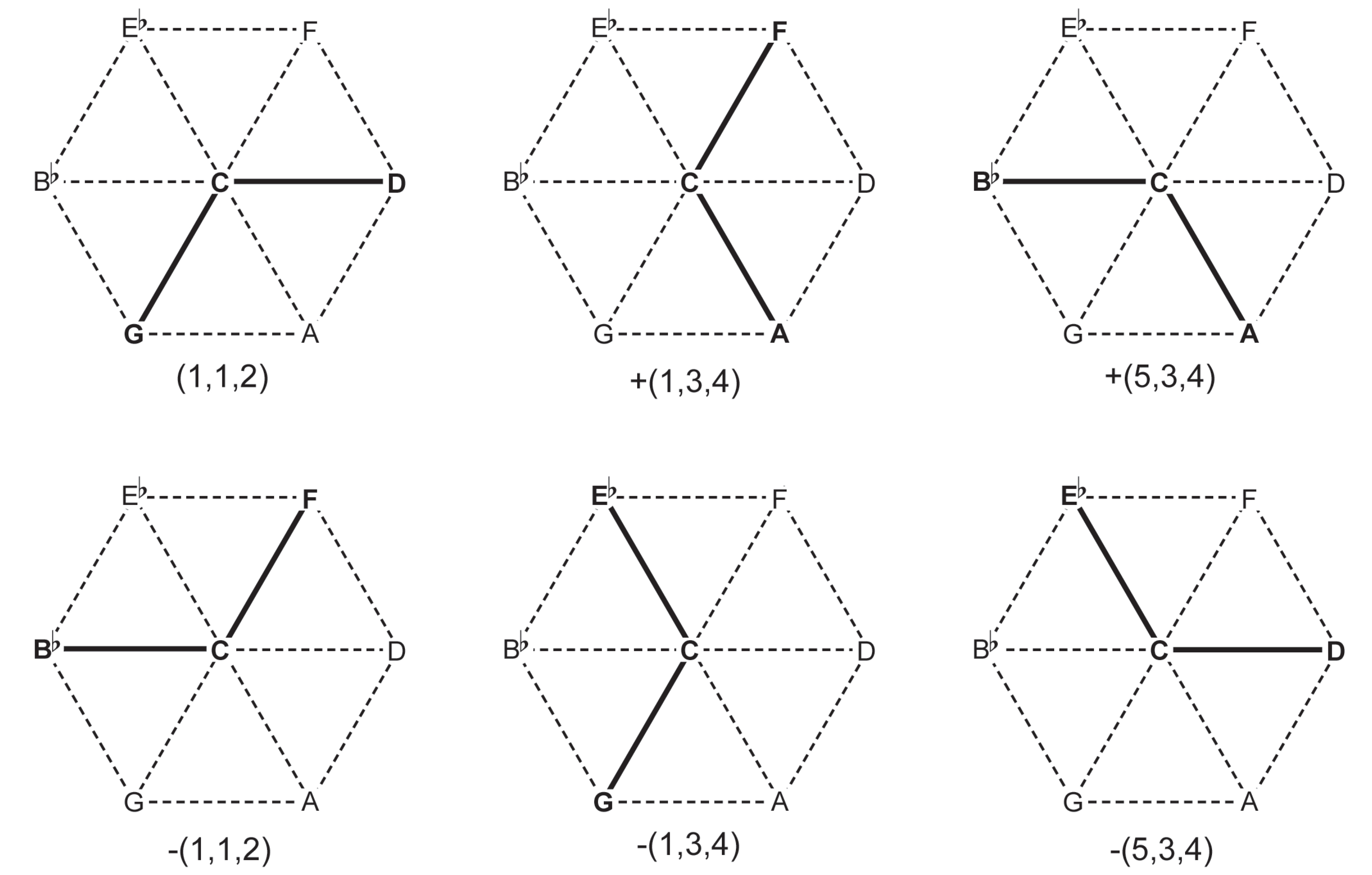
If we take the E which is interpolated within the first frame above, and instead relate it to the adjacent frame, that is, to G and C, the result is a proportional neighbor, (1,3,4). In general, if the interpolated pitches are shifted to occupy the adjacent frames, the result will be a proportional neighbor that shares the framing interval. Below we show the interpolated pitch shifting across four adjacent frames to give us the proportions containing the framing interval class, |1|, in the order they appear in the diagram:

Each interval class (degree of modulation) follows a different distribution in the diagram. The upper row orders the proportional categories that incorporate degree |1|: |1,2,3| - |1,3,4| - |1,5,4| - |1,5,6|. The lower row orders the categories that incorporate |5|: |5,2,3| - |5,3,4| - |1,5,4| - |1,5,6|. The square circuit on the left orders the categories that incorporate |3|: |1,2,3| - |1,3,4| - |5,3,4| - |5,2,3|. The triangular circuit in the middle orders the categories that incorporate |4|: |1,3,4| - |1,5,4| - |5,3,4|. On the very left we have two categories that incorporate |2|. When any one of these intervals is used to modulate and frame a series of proportional categories, the associated sequence of co-derivative categories containing that interval appears in the resulting series of neighborhoods. Finally, there are two non-redundant proportions which derive themselves: |1,5,6| and |2,4,6|. The latter is the only non-redundant proportion that contains no unitary interval classes; it resides in the subgroup of order 6 generated by degree |2|, which may be said to enable a sense of incremental movement due to the quorum of three degree of modulations found in this proportion. However, it is derivationally inert, that is, when modulated by one of its intervals, no other non-redundant proportions appear; this mono-proportional inertia manifests as a lack of functional variety in the corresponding subgroup.

Harmolodic Geometry

Intervallic Vectors and Proportional Lattices

We can visualize harmolodic space by thinking of modulations as vectors that generate a linear sequence of keys:

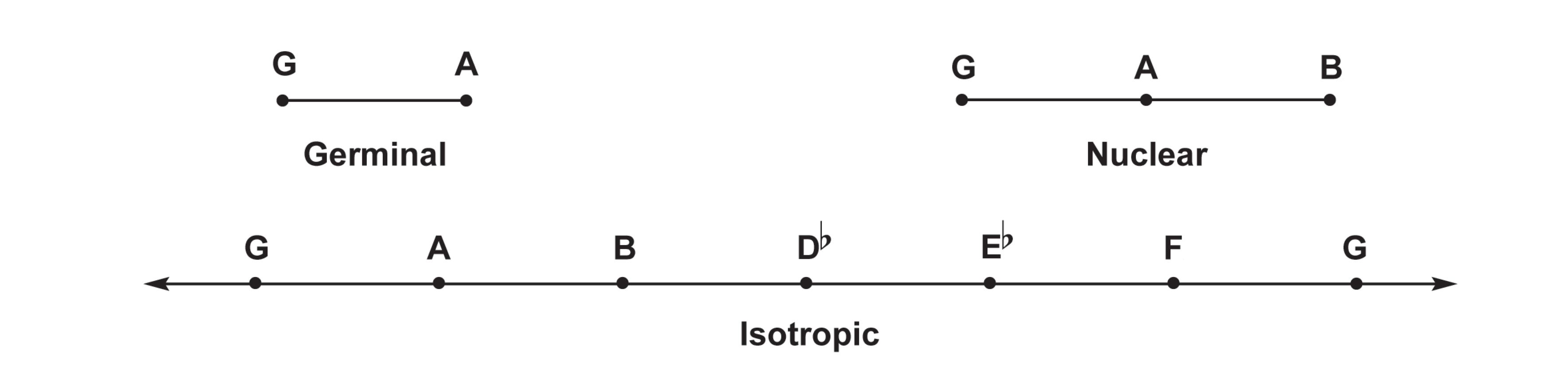
Insofar as these lines can be traversed in either direction, a modulation always appears with its inverse. We have been referring to this undirected modulation as a degree of modulation.

The diagrams above represent degree |2| in three formats. The germinal representation displays the minimum number of keys required to instantiate the modulation. The nuclear representation provides a reference key with the neighborhood of adjacent keys provided by the two inversions of the modulation. Lastly, the isotropic representation displays this neighborhood for each key.

Some proportional categories are already visible in a single linear dimension. Proportions containing a duplicated pitch or modulation can be captured in a single linear orientation. If we assume that null modulation has no linear distance, but simply relates a point to itself, proportions that include null modulation can be captured in the germinal representation of any remaining degree of modulation. Proportions that include a duplicated modulation can be captured in the nuclear representation of that degree of modulation.

To represent non-redundant proportions—those which include three unlike degrees of modulation—we will have to accommodate three independent linear orientations. By arranging the three keys instantiating a proportion at equal distances from one another, we arrive at a germinal representation that integrates three linear orientations within a plane:

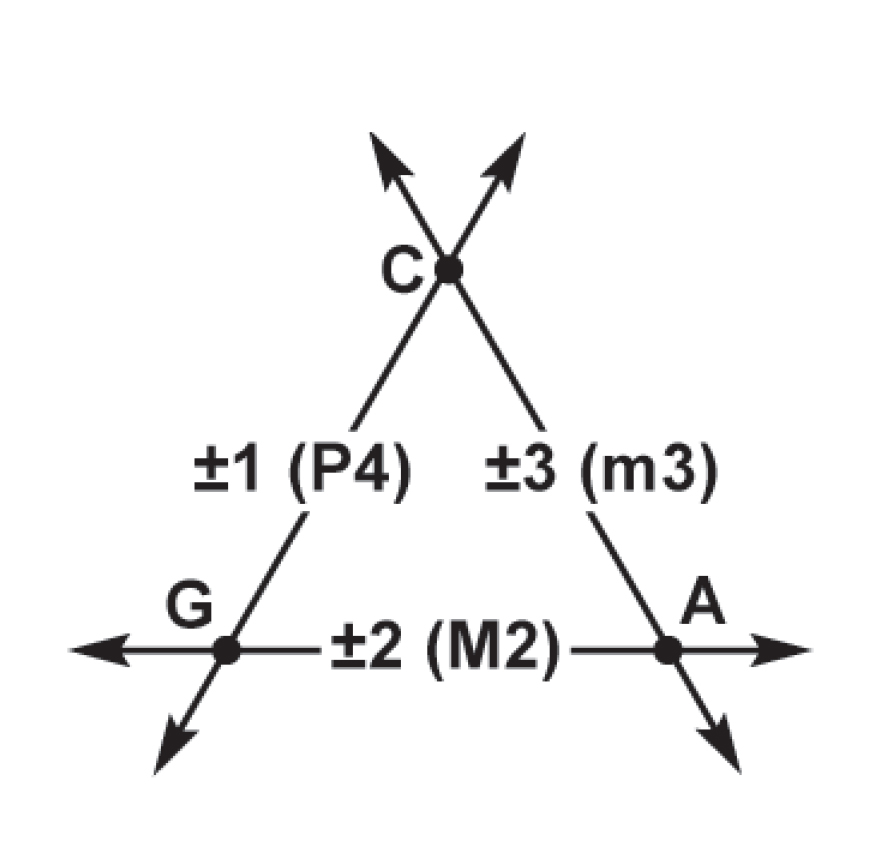
In the corresponding nuclear representation, these three linear orientations intersect a single key, and also form a circuit around six peripheral keys. The central key is surrounded by six proportions of which it is a constituent:

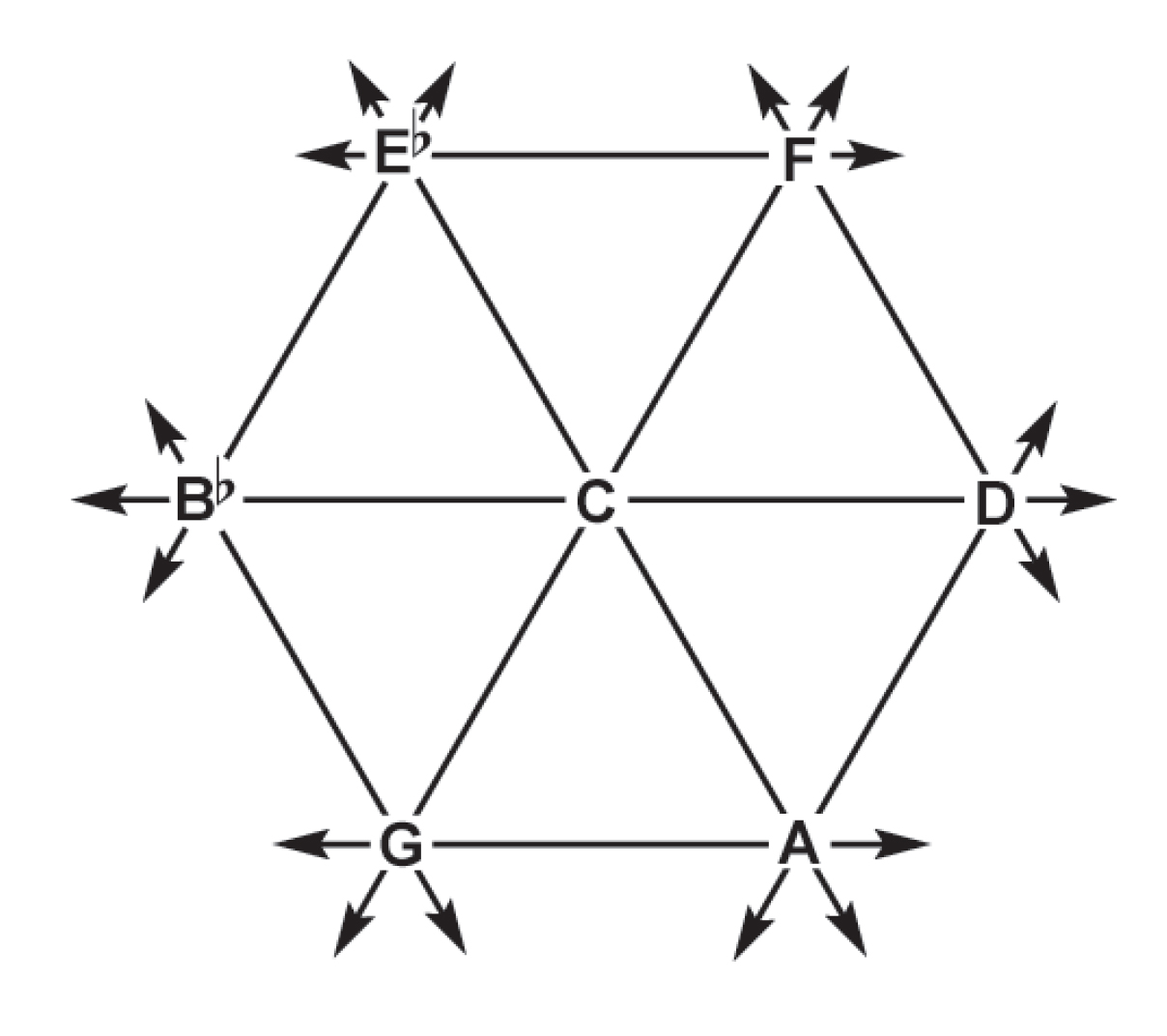
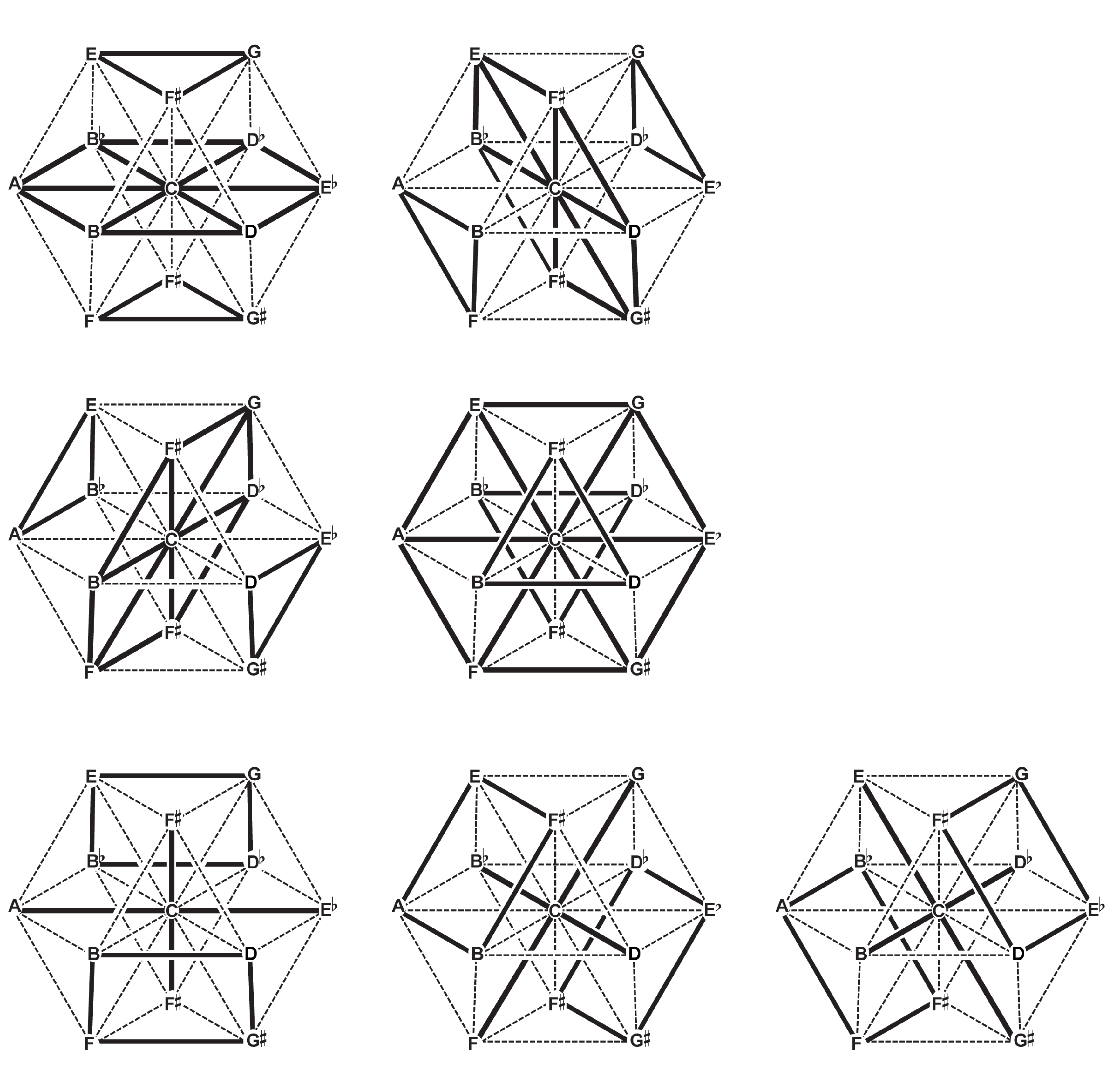
This nuclear key takes on one of the three possible roles in the proportion; in this example, it modulates two other keys by the interval classes +1 and +3, -2 and -3, or -1 and +2. Each role corresponds to one of the three minimum curves found in each proportion. Simultaneously, it completes three forms of the inverse proportion; each upward pointing triangle forms a different transposition of the +(1,2,3) proportion, while each downward pointing triangle forms a different transposition of its inverse, the -(1,2,3) proportion. What we have been calling “proportional categories” encompass the proportions and their inversions that appear together when their constituent modulations are iterated.

Proportional categories sharing two modulations with a given proportional category appear as 120-degree angles in its nuclear representation:

In the isotropic representation of a proportional category, each pitch is situated at the intersection of all three modulation vectors:

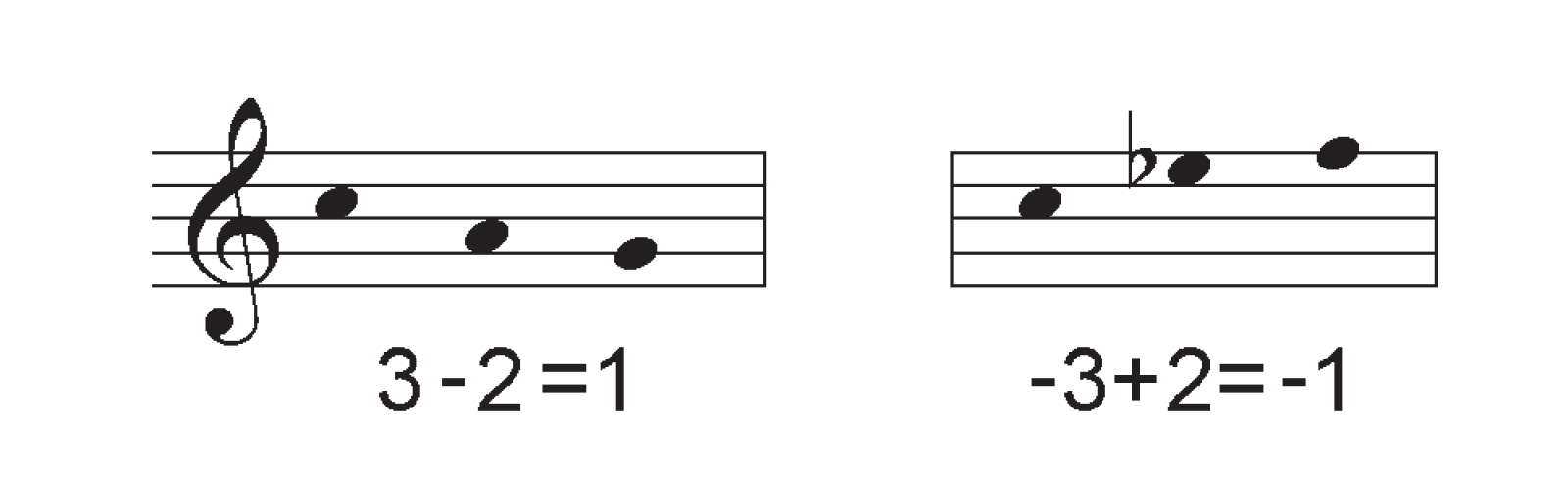
Just as each pitch is adjacent to six others, each proportion is adjacent to six transpositions of itself, and six transpositions of its inversion. Out of these twelve adjacent proportions, it shares an edge with three inversions and a point with the others. A shared edge denotes two shared keys; each edge-adjacent inversion flips the minimum curve that the edge subtends by replacing its pivot key such that the two modulations which it juxtaposes are exchanged:

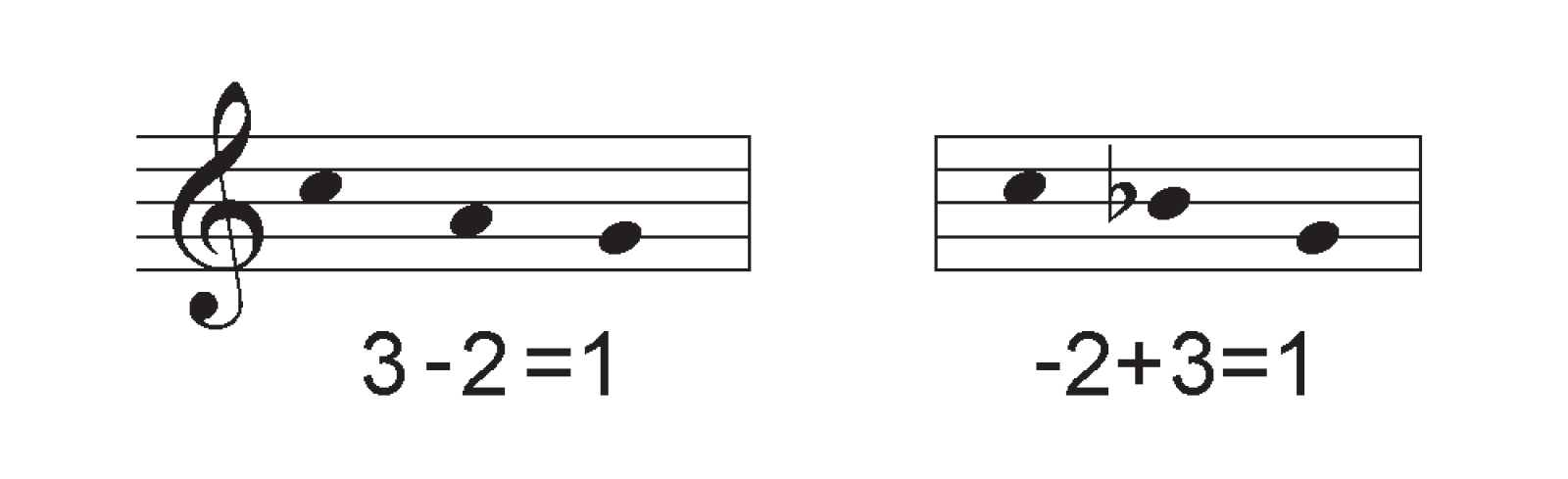
A shared point indicates one shared key—each of these inversions flips the curve that is shunted through that key by replacing its boundary key.

Harmolodic Equilibrium

Four keys coincide six modulations, four proportions, and twelve minimum curves. Hence, a non-redundant tetrachord—commonly known as an “all-interval tetrachord”—will incorporate the full gamut of modulations. There exist four configurations of this gamut. This gamut can thereby be assembled in four possible geometric configurations.

As with our proportional categories, we can obtain a germinal representation of these indexical formats by arranging four points at equal distances from one another, associating each degree of degree of modulation with a unique linear orientation. Four intersecting planes and six intersecting lines are immediately visible in the resulting tetrahedron:

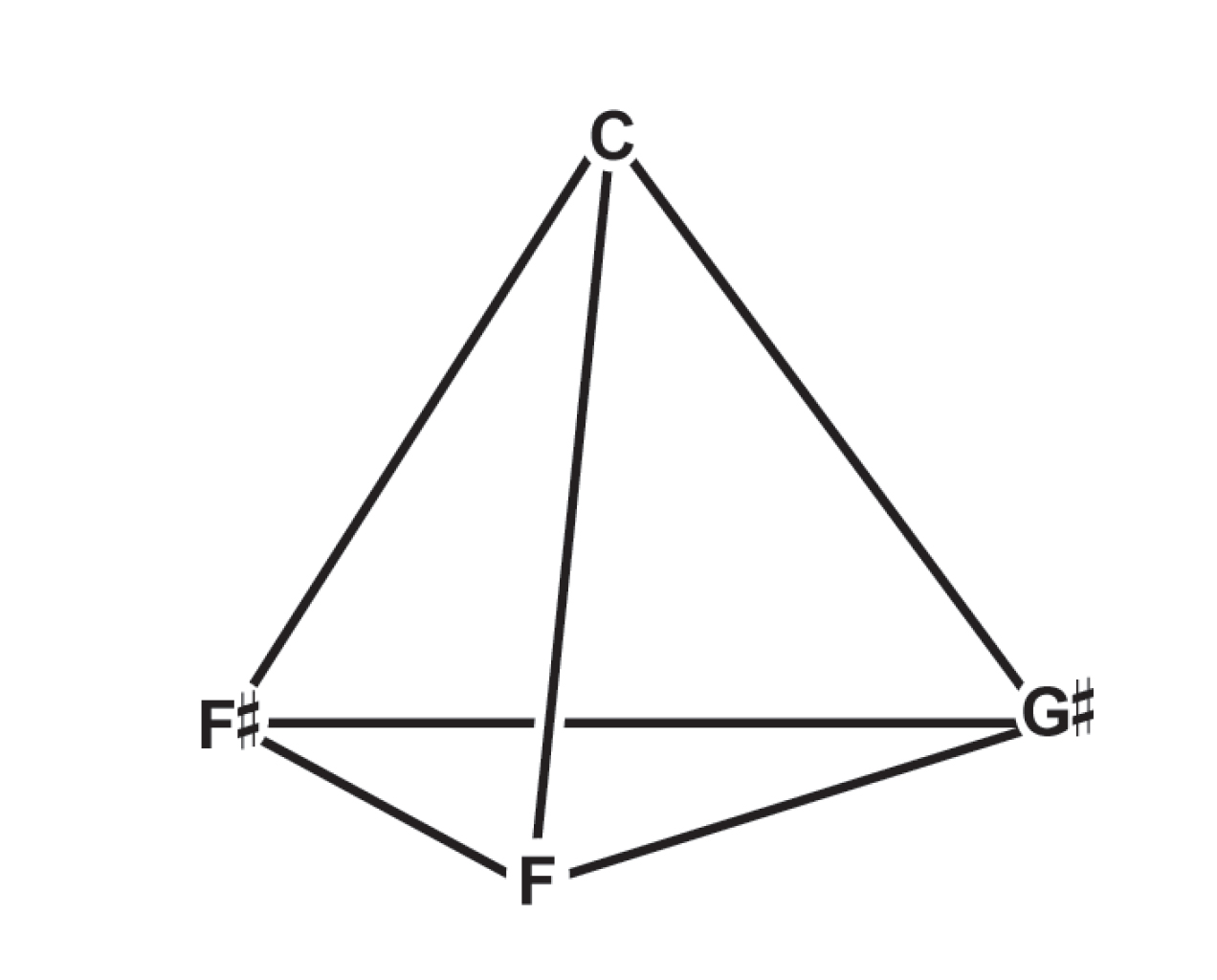
If we extend just three of the linear elements, we see that as with their constituent proportions, these proportional configurations are interwoven with their inverses, giving us just two proportional formats:

While these formats incorporate the same degrees of modulation, their proportional inventories differ:

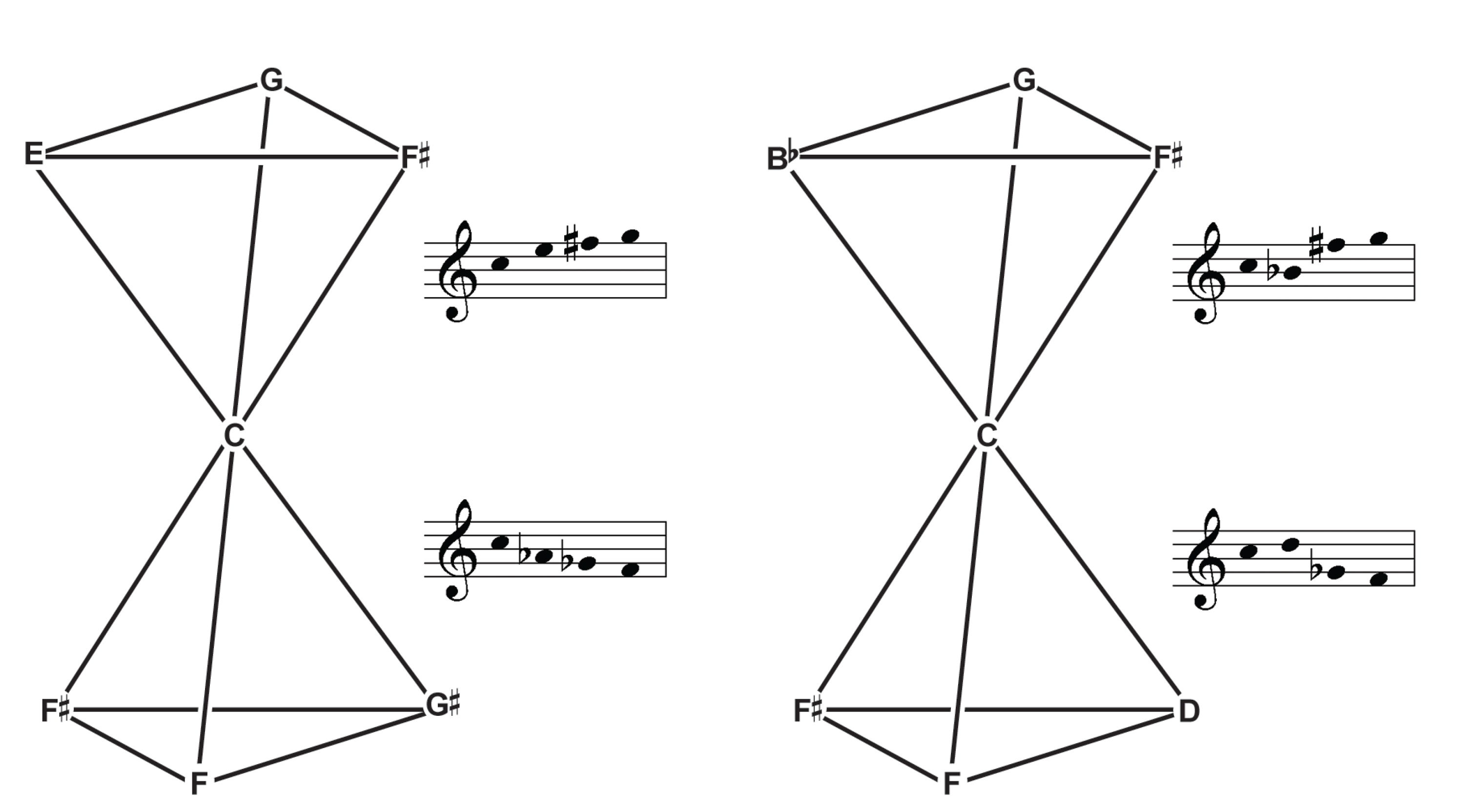
The germinal representation of each indexical configuration precludes co-derivative proportional categories sharing two of three modulations: each constituent trichord of a non-redundant tetrachord shares just one interval class with each of the others, just as in a tetrahedron, any two triangular faces share one edge. If any of the keys in one of these constituent trichords are replaced by the complementary fourth key, two of the modulations necessarily change as well, for each pair of keys is separated by a unique degree of modulation. Below we reproduce our diagram of co-derivative proportional categories twice, circling those that comprise each proportional format:

The full inventory of minimum curves and proportional categories is obtained in the corresponding nuclear representation, in which six degree of modulations and four proportional categories radiate symmetrically from a single point:

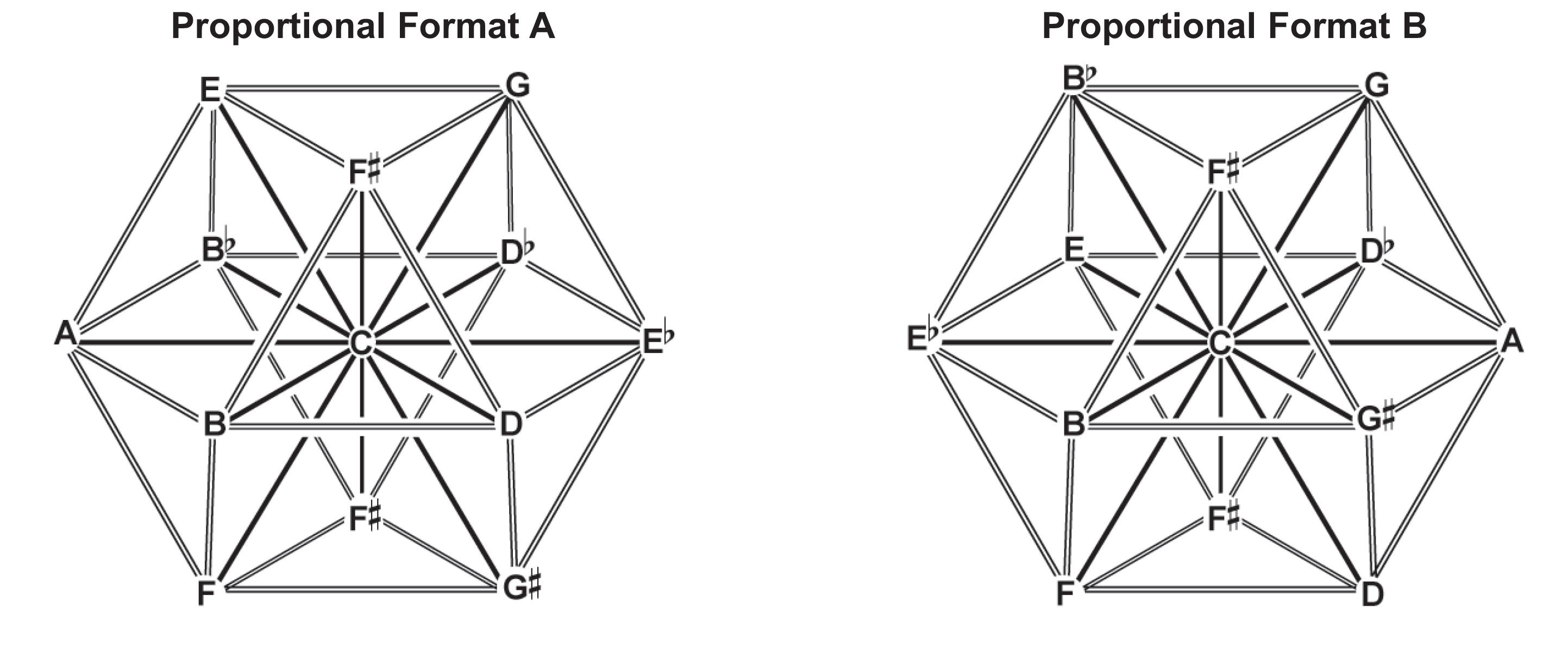
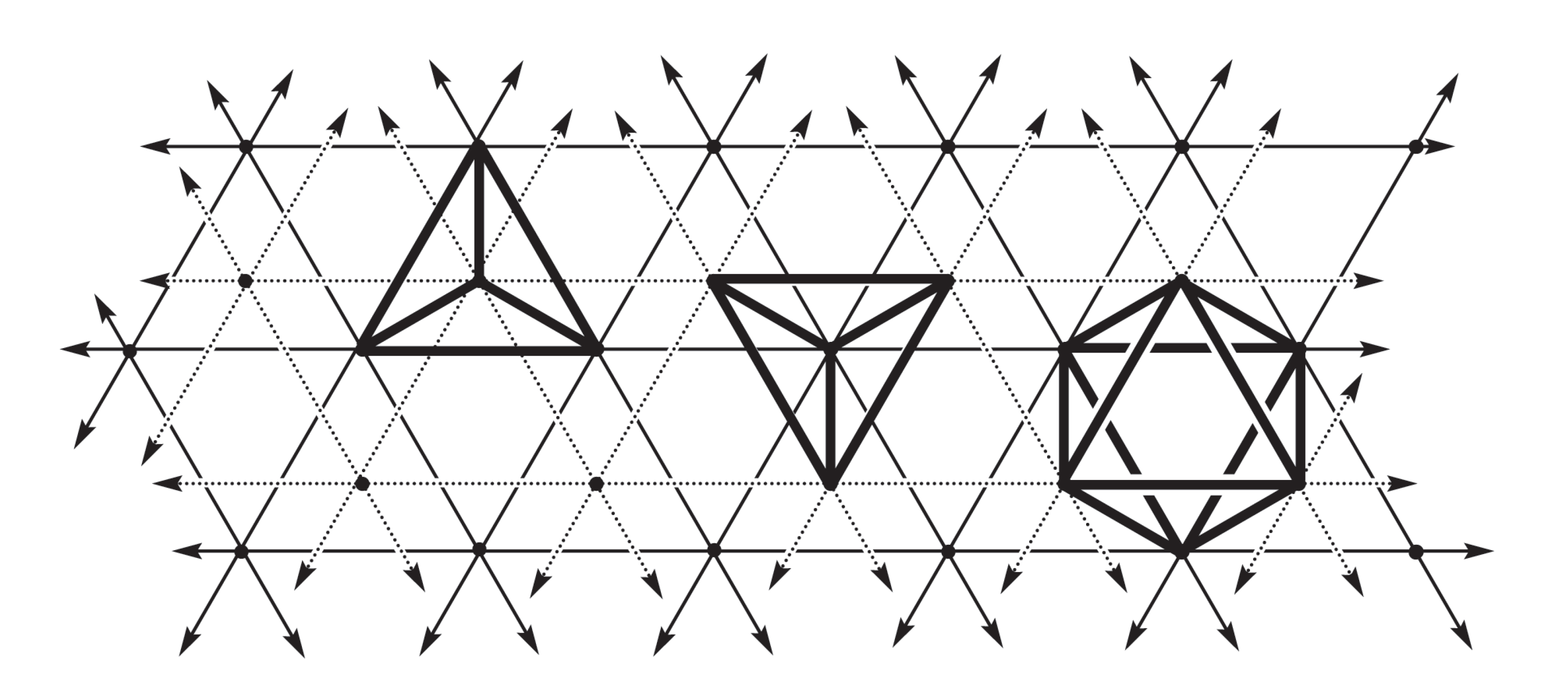
The twelve peripheral keys form a polyhedron called a cuboctahedron. Buckminster Fuller coined the term ‘vector equilibrium’ to refer to this polyhedron when considered together with the internal edges that converge at a central vertex. We can adopt Fuller's term to evoke the essential feature of cardinal harmolodics: it renders every degree of modulation, and by extension every key, adjacent to a given key—and since every note is potentially a key unto itself at the horizon of harmonic intuition according to the harmolodic axiom, this geometry provides each voice with an indispensable compass.

The four primary proportional categories of each format appear in the associated harmolodic equilibrium as four hexagons arrayed symmetrically around the nucleus key. The remaining co-derivative categories appear as 120-degree angles, completing the full inventory of proportional categories. Note that the category |1,5,4| only appears as a 120-degree angle in the harmolodic equilibrium because it never appears in all-interval tetrachords, only in modulations of the latter which share a key. Any two transpositions of an all-interval tetrachord by the degree of modulations |1|, |5|, or |4| will contain the proportional category |1,5,4|.

The duality of proportional formats reflects the dual basis of our dodecaphonic ring, that is, the ability of either |1| or |5| to function as a unit that generates every other degree when iterated. The dualism of the harmolodic equilibrium corresponds to the substitution of harmonic units for gradient units, and vice versa. To demonstrate, we can superimpose the gradient modulation cycle upon the harmonic modulation cycle, assigning each interval class with a counterpart. Each degree of modulation is equal to five of its counterparts.

If each degree of modulation in one of the proportional domains is replaced by its counterpart, the other proportional format results. Likewise, each proportional category in one format has a counterpart in the other by virtue of this substitution:

If |5| appears in a given proportional domain, |1| appears in its counterpart in the other harmolodic equilibrium, and vice versa. If one of the two unitary degree of modulations appears in a given proportional domain, it has an unlike counterpart; if both or neither of the two unitary degree of modulations appear, then it is its own counterpart.

Each edge in a tetrahedron is separated from an opposing perpendicular edge. Equivalently, within a proportional format, any given modulation is disjunct from the modulation that separates the remaining two keys. Of the six degrees of modulations in a proportional format, there are then three pairs of disjunct modulations. However, all six degrees of modulation intersect in the nuclear key of the vector equilibrium. The latter combines each of these pairs in an additional rectilinear plane of symmetry:

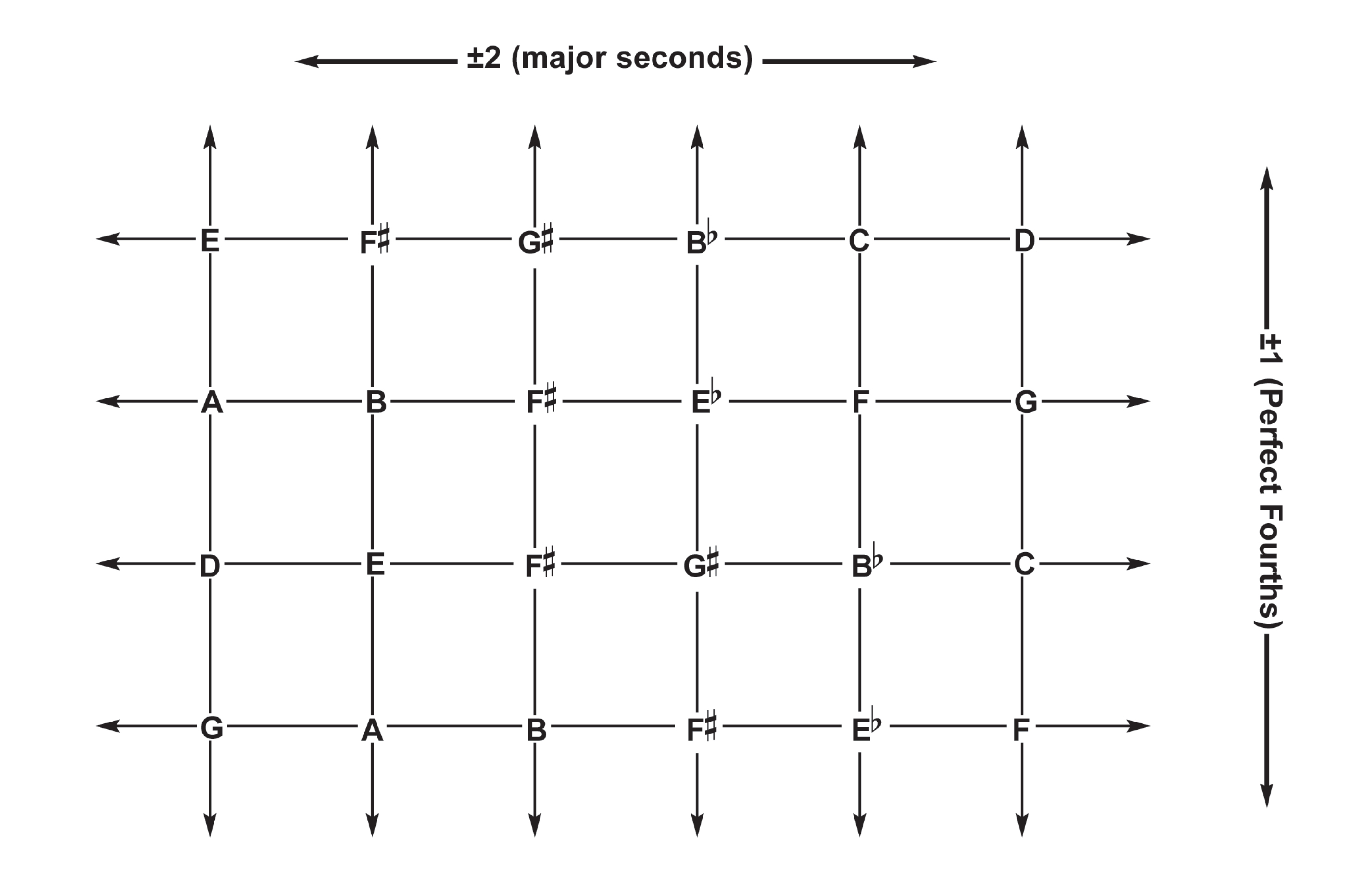
These additional proportional categories are made overt through a transformation of the harmolodic equilibrium dubbed the “jitterbug” by Fuller, whereby each square face of the harmolodic equilibrium buckles until it forms two equilateral triangles constituting a proportion and its inverse (the second proportional category found in each rectilinear orientation becomes a 120 degree angle, forming a co-derivative proportion). The twelve new triangular faces along with the changes in angle effected by the deformation produce an icosahedron. In addition to the 4 primary proportional categories found in the tetrahedron, this icosahedron includes the category |1,4,5|, that member of the unitary dual |1,2,3||5,2,3| which is not found in the primary inventory, and a proportional category from the diminished subgroup |3,3,6|.

The jitterbug transformation doesn't stop there - it continues to compress the shell of the harmolodic equilibrium into a variety of polytopes in which the vertices attain an equilateral triangulation, and converge to a smaller set which identifies certain pairs, triples, and quadruples of key. These polytopes include an octahedra in which the vertices are pairs of keys manifesting a modulation, and tetrahedra in which vertices are triplicities of key manifesting a proportional category. Outside of the platonic solids, the harmolodic equilibrium can also be transformed in triangular dipyramids, pentagonal dipyramids, square pyramids, two square pyramids linked at a vertex, two square antiprisms, truncated triangular pyramids, and so forth. In effect, the jitterbug can function as a tool for exploring a wide range of surjections from unitary key space into smaller cardinalities combining various keys—a bonus of unknown potential.

The harmolodic matrix

In total, then, the harmolodic equilibrium has seven planes of symmetry:

A final elaboration of harmolodic geometry, every key is identically situated at the intersection of six linear paths and seven planes. This expanse is conventionally known as a ‘face-centered cubic lattice’; we will again follow Fuller's more singular and evocative term ‘harmolodic matrix’ . To construct it, we can start with one of the of triangular planar arrays. When we juxtapose each instantiation of a given proportion with its complementary fourth key, situating the new pitches equidistantly from each of the three pitches they complement, the new pitches form a planar array which is parallel to the first, replicating its proportional category:

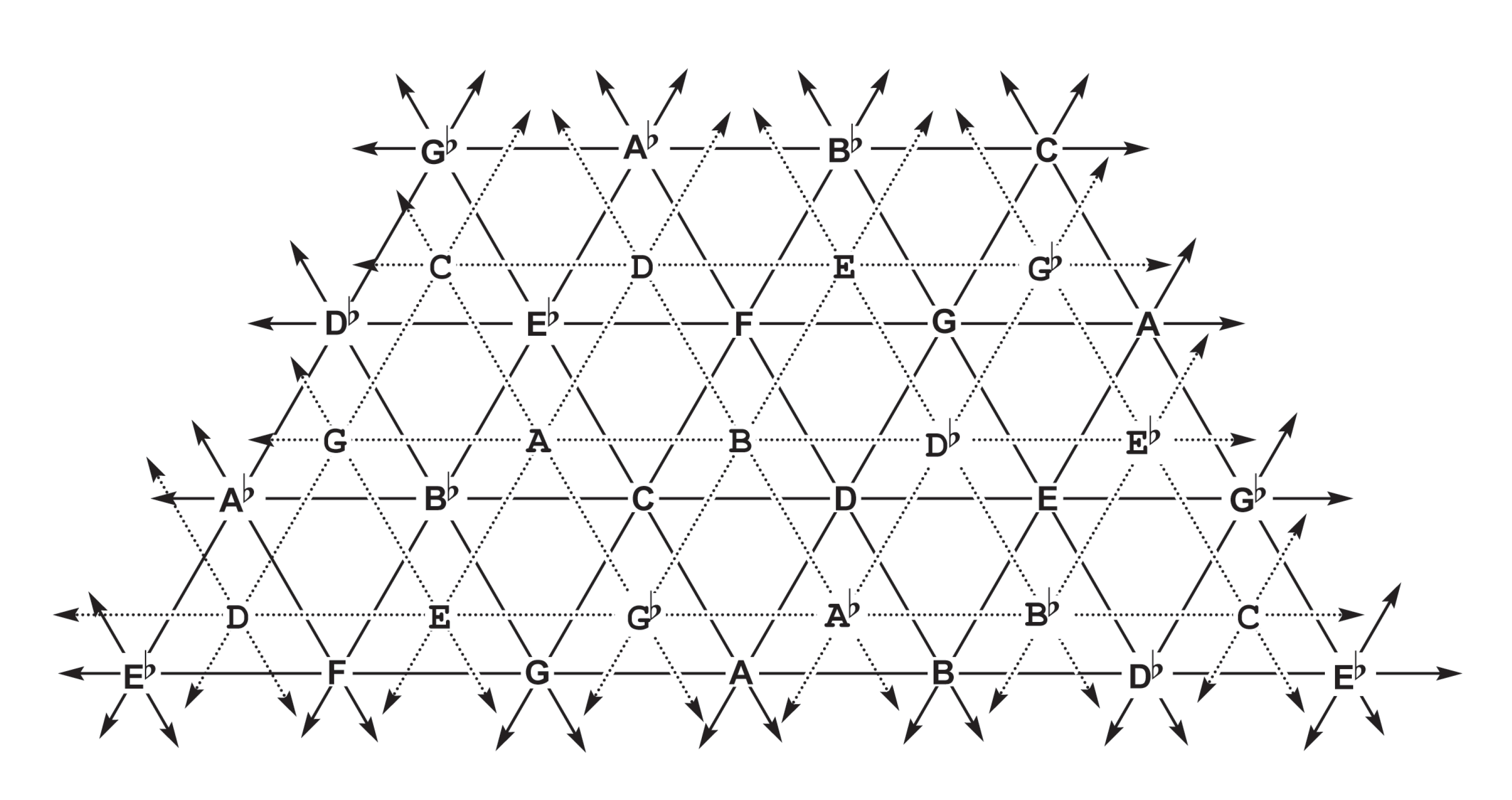
The keys that complement the inverse trichords are located in the opposite direction—if the complementary keys of one proportion form a superjacent layer, then the complementary keys of the inverse proportion will form a subjacent layer. Analogous layers can be stacked in both directions infinitely.

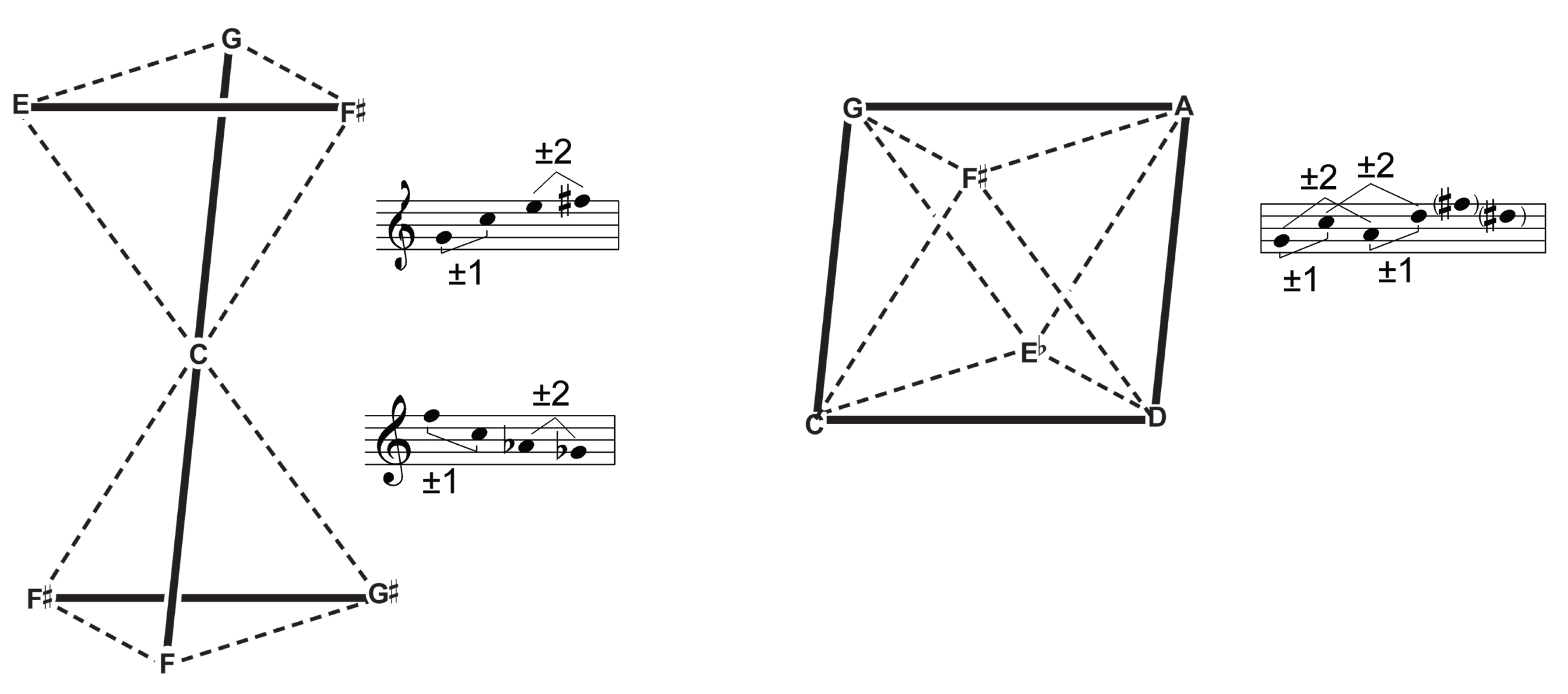
We can outline the atomic cells that constitute the harmolodic matrix by connecting the keys of the superjacent layer to the adjacent keys in the first layer. Firstly, an array of tetrahedra points from the original triangular array towards the viewer. Secondly, an array of inverse tetrahedra points from the superjacent triangular array away from the viewer. Finally, the negative space between the tetrahedra is comprised of octahedra.

Each proportional category constitutes the face of a tetrahedron in one direction, and the face of an octahedron in the other direction.

We can visualize the three planar orientations which are not parallel to the page converging on one side of a given proportion to enclose a tetrahedral space, and diverging on the other side to make room for an octahedral space; the same proportional fields converge and diverge in opposite directions from the inverse proportion.

The octahedra combine precisely the modulations that are disjunct in the tetrachord; each degree of modulation appears twice and is doubly linked to its estranged counterpart in the hexachord corresponding to the octahedron:

Summary

The harmolodic matrix presents no restrictions on the ordering of a pitch set (each member of which is a key center unto itself, axiomatically). Rather, it represents the interval classes as twelve cardinal directions surrounding every pitch. Thus, every ordering of every pitch set is a contiguous trajectory in the harmolodic matrix.

The salience of a musical figure is a reflection of its intervallic constitution, not its pitch constitution: we hear different transpositions of a musical figure as the same thing because the intervallic relationships within it are the same. The two transpositions sound different only insofar as they are juxtaposed so that we hear a further interval between them (the ability to identify absolute pitch, inexplicably revered in the music world, is nothing but episodic memory, which provides this same juxtaposition introspectively).

Each order of difference is deferred to a higher dimension of Eulerian topology. A vertex is a single note, which is a single key; it is a placeholder for musical form in that it is equivalent to any other key but for its modulation. A second key traces an edge, which is the difference introduced by its modulation. With three keys/notes, three intervallic functions outline a face, which expresses the concomitance of their proportional relationships. With four keys/notes, four proportional bundles give us a complete inventory of the preceding elements. The fourth degree is the terminal, insofar as five keys necessarily contain replicated modulation and proportion, which are already expressed in the extension of the existing edges and faces.

If we try to parse a musical passage into the smallest intervallically identical forms recurring in various transpositions, we're left with trichords, which uniquely present both the incipient musical identity found in a minimal composition of intervals and the distinctive partiality of a maximal proper subset of the intervallic gamut.

If intervallic functions differentiate notes, and the proportions differentiate intervallic functions, the harmolodic equilibrium encompasses every difference at once. The two proportional formats, when indexed by all-interval tetrachords, are an elegant and intuitive representation of the gamut of proportions.

Modulatory/intervallic vectors can operate either as radial or compressive forces. The modulation of a musical figure is its radiation away from the reference point along an axis which represents a consistent degree of difference. This linear movement away from a key can be shunted along a new degree of difference, exchanging radial energy for an elaboration of structure. A persistent elaboration of structure outlines concentric polygonal and polyhedral shells that restrain or moderate the linear momentum of a repeated modulation.

Serialism, for instance, prototypically utilizes the most compressive form within the harmolodic matrix, namely, the vector equilibrium. To be more precise, since the degree of modulation |6| replicates the same pitch class on either side of a nuclear pitch class, each instance of a tone row can be obtained in a nuclear pitch class along with eleven surrounding pitch classes—a ‘dimpled’ vector equilibrium. While a given twelve-tone row doesn't necessarily follow a contiguous trajectory around this form, its pitch classes do form a relative locality within a composition which constitutes this maximal elaboration and compression of interval structure. The unrelenting recurrence of this maximally compressive form conveys a monotonous pervasion of harmonic torque that actually serves to render unserialized aspects of form such as gesture more conspicuous; on the other hand, the internal permutations of the form, by providing fleeting glimpses of radial momentum, confer a pittance of variety at the most local scale of magnitude.

Harmolodic Composition

Whereas the harmolodic matrix condenses intervallic and proportional rudiments isotropically around each position, without specifying order or taking their appearance in time into account, we will now consider the various orderings of the proportions insofar as they form the genetic basis of composite events. In the previous section we preferred the terms ‘key’ and ‘modulation'; moving forward we will revert to the more intuitive and harmolodically equivalent terms ‘pitch’, or even ‘note', in the understanding that every pitched note, together with its pitch class, is treated with respect to its own tonal center of gravity, and is essentially the minimum instantiation of a key, and ‘interval’, which is axiomatically understood to relate two autonomous pitch classes, so as to abstract its modulatory function from the scalar change in frequency produced by the registers used in that particular instance of its interval class. Analogously, the term ‘trichord’ will be used interchangeably with ‘proportional class’.

Ornette Coleman's seminal composition for orchestra, Skies of America, illustrates the differential basis of harmolodic quantity elegantly. Coleman declined to compensate for the divergent clefs and instrument transpositions that inhabit the European orchestra, exposing a latent harmonic world in its social and historical embodiment. His musical firmament unfolds along two orders of difference: intervals, which measure the difference between pitches, and curvature, which measures the difference between intervals. Each pair of instruments is related by an interval which reappears at each melodic step. Conversely, each note of the melody is reached by an interval that appears in every voice. This null curvature allows the resonance of the orchestra to pervade each musical event. As the piece unfolds and voices begin to diverge from the surrounding parallelism, advancing by a different melodic interval than their conspecifics, their mutual distance also modulates by this second-order difference between intervals, or curvature. Every possible musical event is an aggregate of such modulations, and each one isolates a unique and salient musical intuition from the infinite combinatorics of discrete twelvefold structure.

Non-Linear interval sequences

The harmolodic matrix comprises every pitch sequence constructed from a constant interval. These sequences are linear in the sense that they have no curvature, that is, no difference between successive intervals. We could also construct second-order linear sequences of constant curvature, in which successive interval classes change by a constant value. Whereas the linear elements of the harmolodic matrix exhibit constant first-order difference and zero second-order difference, these sequences exhibit constant second-order difference and zero third-order difference:

Curvature is effected in this sequence through the covert presence of trichords: each successive step between two adjacent pitch implies a third, mediating pitch, namely, the pitch one would arrive at if the preceding interval in the sequence were repeated. The pitch one arrives at instead is always separated by the same interval class, not from the initial pitch, but from this mediating pitch.

Ordered trichords can be thought of as directed minimum curves that measure a change in modulation. Their constituent intervals assume three distinct roles:

They form a minimum hierarchical constituency (henceforth, arborescence) in which an interval is bisected into two sub-intervals. Any two of the interval classes determines the third. Using these three positions as a basis, we can define a family of non-linear interval sequences, that is, sequences without any constant degree of difference. Whereas the linear components in the harmolodic matrix exclude curvature, these continually twisting sequences exclude linearity in favor of curvature in every order of difference.

To construct such a sequence, we start with any directed minimum curve. A fourth note is added which modulates the third note by the same degree as the total interval between the first and third notes, accelerating the curvature of the line by encompassing the two preceding intervals in a single step. The second, third, and fourth notes form a new trichord which can be extended analogously, and so forth. Such a sequence displays a perpetually accelerating curvature:

After applying this operation 24 times, one arrives back at the original curve, forming a cycle of intervals which accelerates into itself. Two species of such non-linear sequences exist, each of which can be inverted, for a total of four directed (reversible) sequences. Whereas the harmolodic matrices inventory the proportional categories in an unordered format, these sequences inventory them in an ordered format; each of the six directed curves bundled in each proportion appears twice.

The sum of two consecutive intervals is equal to the interval that follows them; equivalently, the difference between two consecutive intervals is equal to the interval that precedes them. The differences between successive values of the sequence is therefore the self-same sequence: the sequence of intervals, curvatures, third-order differences, and so forth, are identical.

Linear sequences all reduce to a constant, that is, zero on some order of difference: a pitch repeats, always changes by the same interval class, the change in consecutive interval classes remains the same, et cetera. In contrast, non-linear sequences are derived through an operation on the variables captured in the addresses within a directed minimum curve, without any reference to a constant, and so are not reducible to zero.

Non-linear interval sequences include intervallically redundant proportions, but exclude those proportions which appear in the subgroups generated by non-unitary intervals: symmetrical senary pitch space (whole-tone intervals), quaternary pitch space (diminished intervals), ternary pitch space (augmented intervals), binary pitch space (tritone intervals), and unary pitch space (null intervals). If a minimum curve does not contain a unitary interval, |1| or |5|, then it does not appear in the sequences above, but in analogous non-linear sequences of reduced cardinality:

Among the duodenary sequences expressing unitary intervals, henceforth ‘unitary sequences’ (not to be confused with the trivial and degenerate unary sequence of null intervals), we can observe that the A sequences monopolize null interval, |0|, while the D sequences monopolize antipodal interval, |6|. When a null interval is followed by any other interval, the resultant total interval is identical to the latter. As a result, the A sequences also have the monopoly on the redundant unitary proportions |1,1,2|, |5,5,2|, |0,1,1|, and |0,5,5|. In each case the redundant interval is a harmonic or gradient unit—the other redundant proportions appear in the non-linear sequences of reduced cardinality. On the other hand, the D sequences contain every instance in which both unitary intervals appear together in a minimum curve, that is, every appearance of the |1,5,4| and |1,5,6| proportions.

Non-Linear Interval Matrices

No specific curve is necessary to germinate these non-linear sequences—any directed minimum curve, operated upon appropriately, will derive one of them. While no single curve is primary, they are each uniquely located, such that they can each be assigned an address:

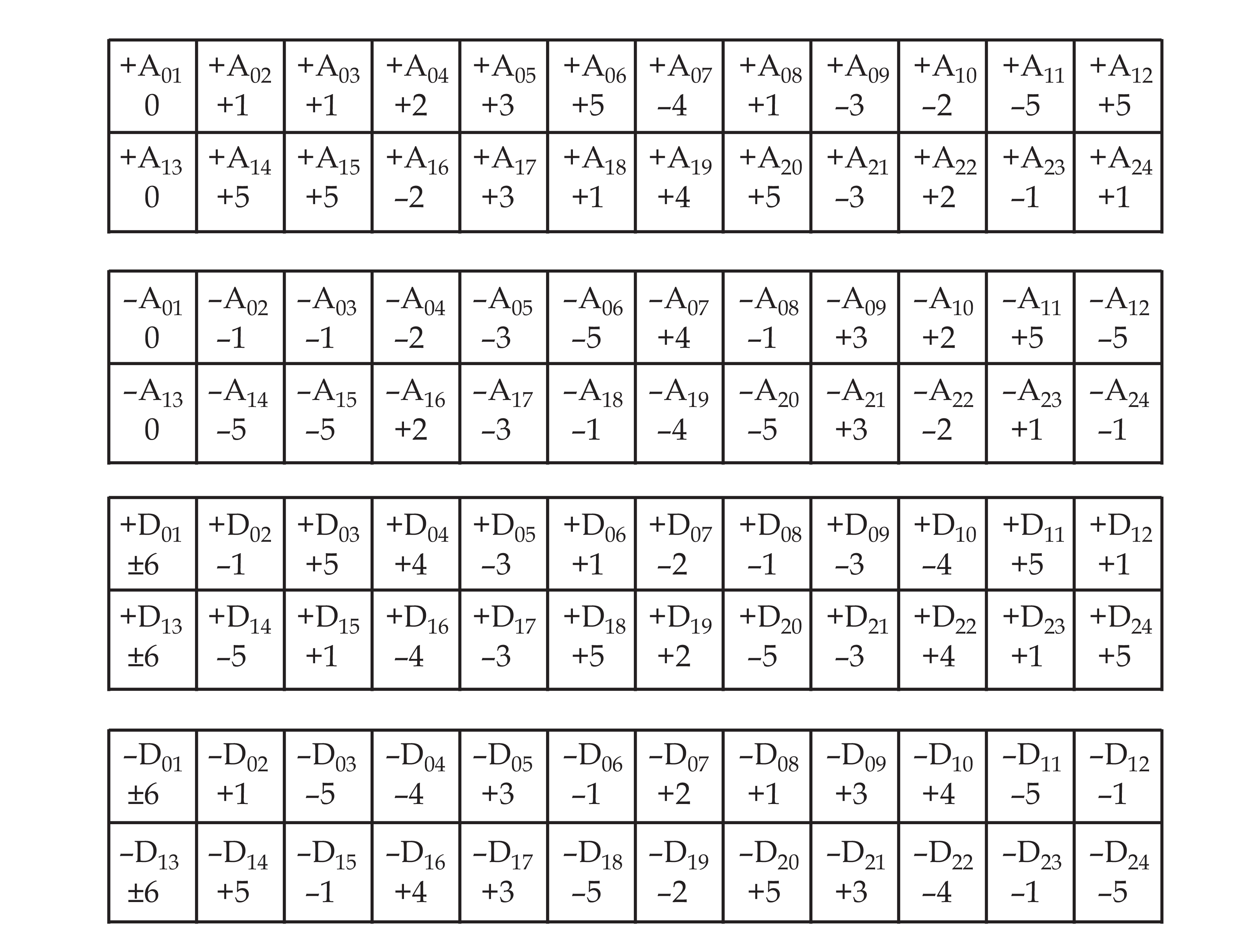
These positions are interwoven. If we take every seventeenth value of a sequence (that is, if we move backwards five steps at a time) the resultant twenty-four value sequence is identical to the original. As a result, every position has a twin somewhere in the same sequence that bears the same value. There are 9 pairs as well as 6 solitary positions that pair with themselves.

We can represent this self-intersection of the unitary sequences by stacking them in another dimension, offsetting it by five indexical positions on each layer, to obtain a two-dimensional matrix which places each pitch class at both of its indexical positions simultaneously:

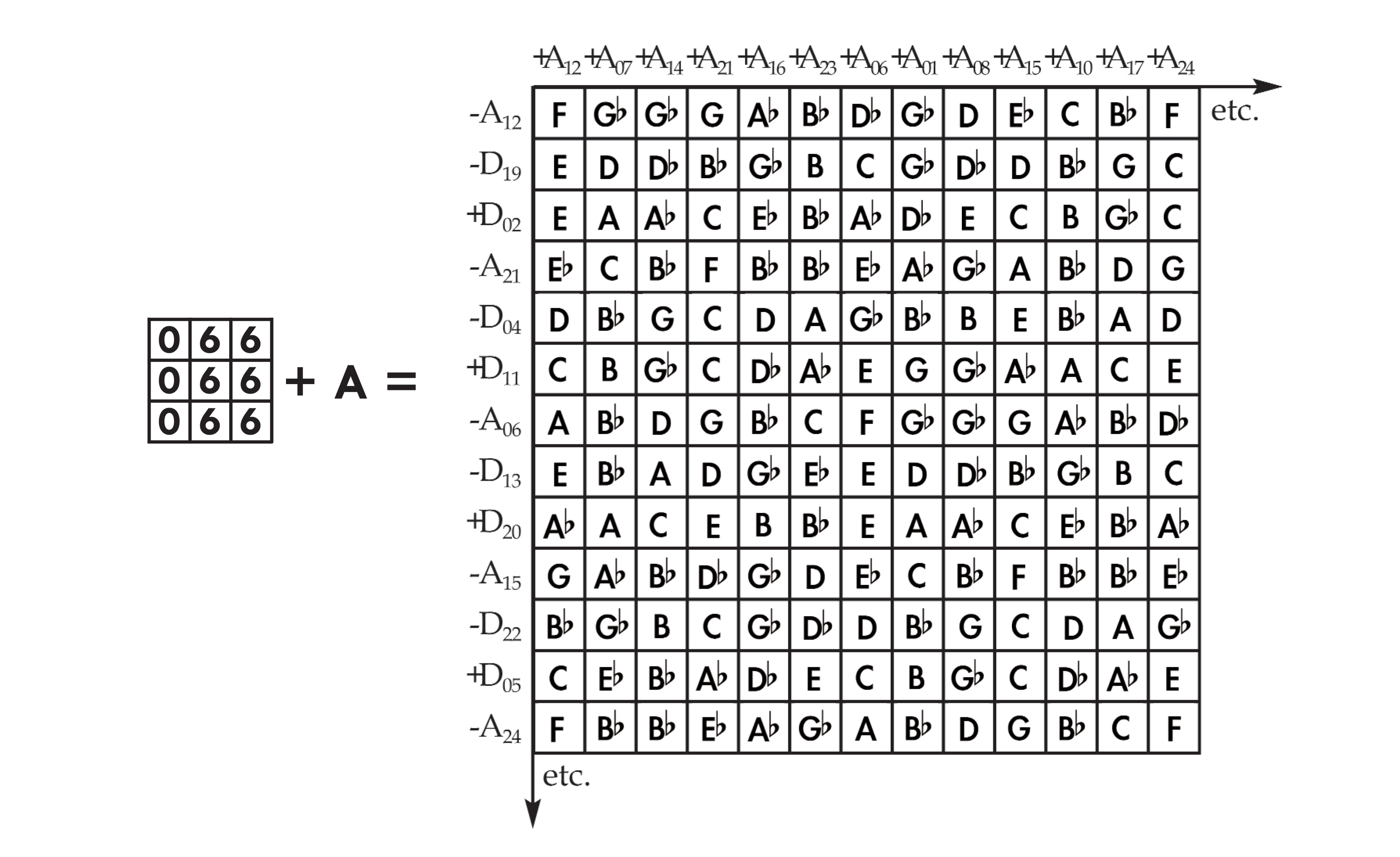
These sequences of intervallic operators can modulate a sequence of notes, that is, measure the distances to a second sequence of notes. In the above matrix, each row is transposed by the intervals in the +A sequence to obtain the next row, as is each column. The matrix is vertically and horizontally saturated by the +A sequence.

The addition and subtraction of non-linear sequences can be generalized; the sum or difference between successive values in two non-linear sequences always constitutes a third sequence which is also non-linear. In other words, these sequences form an abelian group. For instance, the table below shows the sum of each of the unitary sequences and the +A sequence, at each indexical degree:

If two superimposed unitary sequences are offset either once or twice by ±1, ±5, ±7, or ±11 indexical degrees—that is, once or twice by an amount which 24 does not divide into—their difference will also be one of the four unitary sequences; otherwise, the difference reduces to a non-linear sequence of lower cardinality. One can superimpose up to three unitary interval sequences, offset by two equal indexical shifts, and obtain vertical relationships which also instantiate unitary interval sequences; any fourth interval sequence will produce vertical relationships of reduced cardinality with at least one of the other three sequences.

This means that proportions are the largest structures which effectively exclude proportions of reduced cardinality. They delimit the domain that incorporates harmonic and gradient units. Every three by three square on the self-intersecting unitary matrix represents a basic unitary intersection of minimum curves.

The binary or ‘antipodal’ non-linear sequence is the minimum non-degenerate non-linear sequence; this sequence of three values intersects itself in a three by three matrix which matches the perimeter of purely unitary organization just described. When it is applied as an intervallic operator on a unitary sequence it modulates the latter into one of the other three unitary sequences. That is, the sum of the binary sequence and a unitary sequence is always one of the other three unitary sequences, according to the relative indexical position of the addenda:

The four unitary sequences can be integrated by modulating a unitary matrix with a binary or ‘antipodal’ matrix. For each unique self-intersection of the binary sequence within a three by three matrix there is a unique integration of the four unitary sequences. One such configuration modulates the +A matrix so that the +A sequence is interwoven with two other unitary sequences in equal proportions:

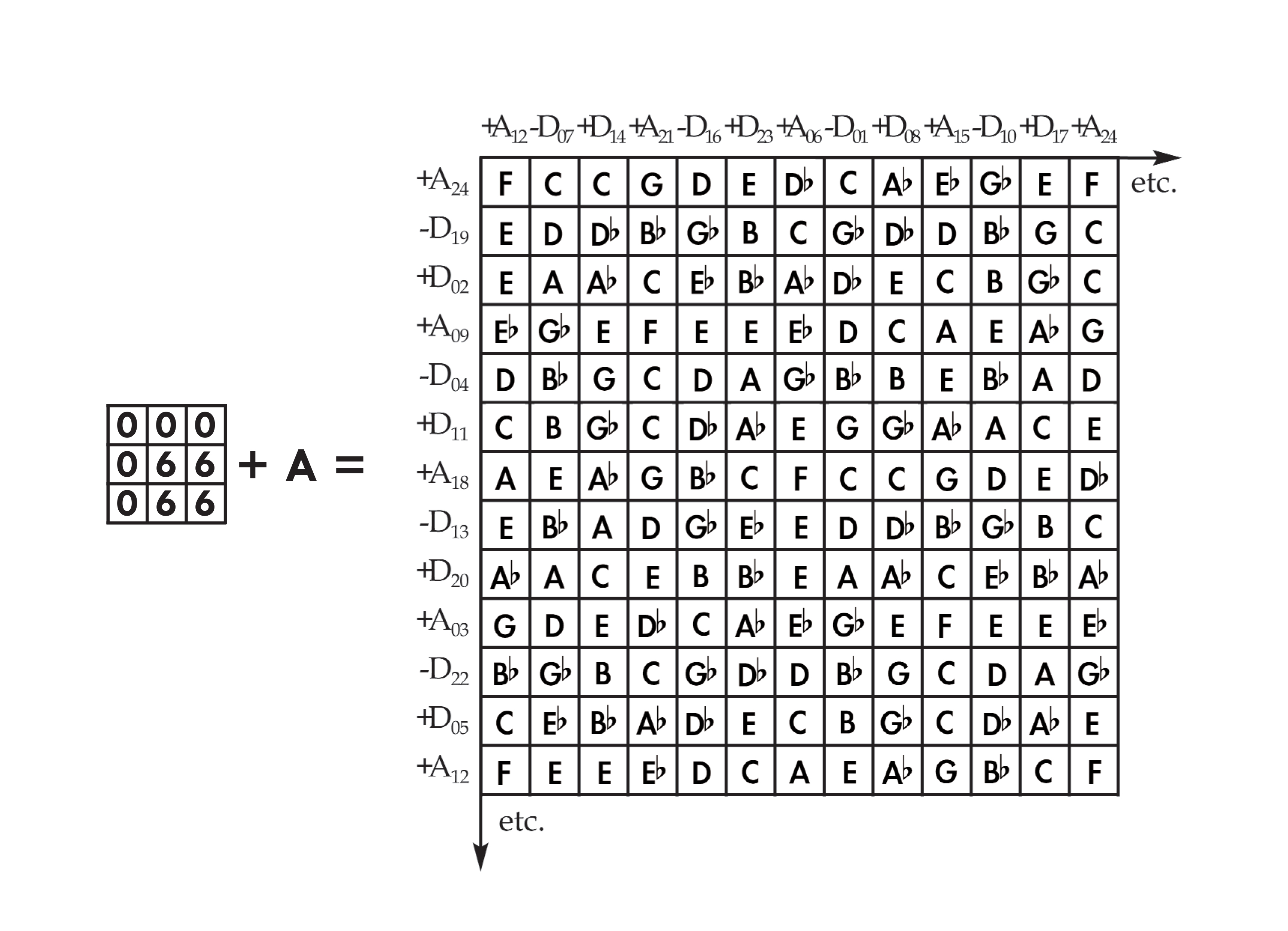
A different binary configuration modulates the +A matrix so that the +A sequence is intersected by the other three unitary sequences:

These configurations can be combined in three dimensions to achieve an integration of all four sequences which retains the asymmetry of the antipodal non-linear sequence. As a practical alternative, one can simply place a pair of antipodal pitchs at each index as a shorthand for a full integration of the four unitary non-linear sequences:

These pitch pairs can be filtered by 3 x 3 antipodal matrices that select a pitchs from each underlying pair within the perimeter of unitary organization. These antipodal filters can rove through a unitary matrix to create sequences of unitary intersections of minimum curves.

Since each pitch is accompanied by the antipodal pitch, we can also arbitrarily restrict our selection of notes to one of any two self-complementing hexachords, simply by modulating to the appropriate unitary sequence at a given point in time, or equivalently, by filtering it through the preferred antipodal matrix. In general, matrices of a given cardinality transpose the notes in a unitary matrix within a symmetrical subset of pitch classes, effectively making it possible to isolate self-complementing subsets of intervals or pitchs and articulate them non-linearly.

For instance, the senary non-linear sequence modulates the unitary sequences by whole-tone intervals, and the range of results can be merged in a matrix where every index is occupied by one of two senary pitch spaces (whole-tone scales). The alternation between these subspaces is isomorphic to the antipodal sequence, and the alternation between antipodal pairs in our shorthand unitary sequence is isomorphic to the senary sequence. We can summarize by saying that unitary non-linear matrices can be decomposed into senary and binary matrices, one of which selects from a hexatonality and its complement, and the other of which selects a pitch from the hexatonality.

The ternary and quaternary sequences, also corresponding to complementary factors of 12, have a similar reciprocal relationship.

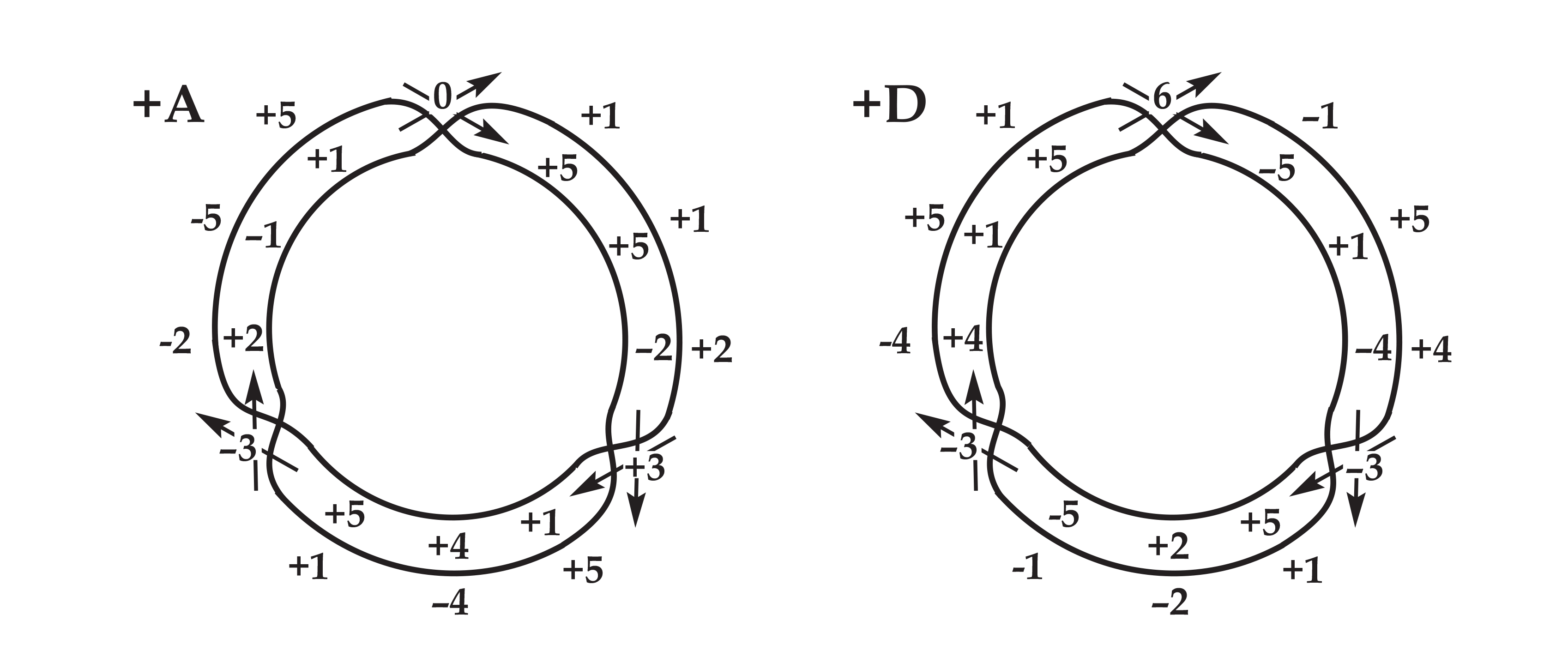
Earlier we observed that each of the two proportional domains can be derived from the other by substituting gradient units for harmonic units, and vice versa. Modulating a unitary sequence by a ternary sequence effects this substitution in non-linear interval space, selectively modulating pitchs by the degree of interval |4|. The substitution of gradient and harmonic units with one another, on the other hand, derives the self-same sequence, shifted by twelve indexical positions, that is, halfway through the cycle. The unitary sequences can be visualized on the surface of a Moebius strip, where each pair of unitary counterparts is allocated to the opposing faces of a given position along the strip:

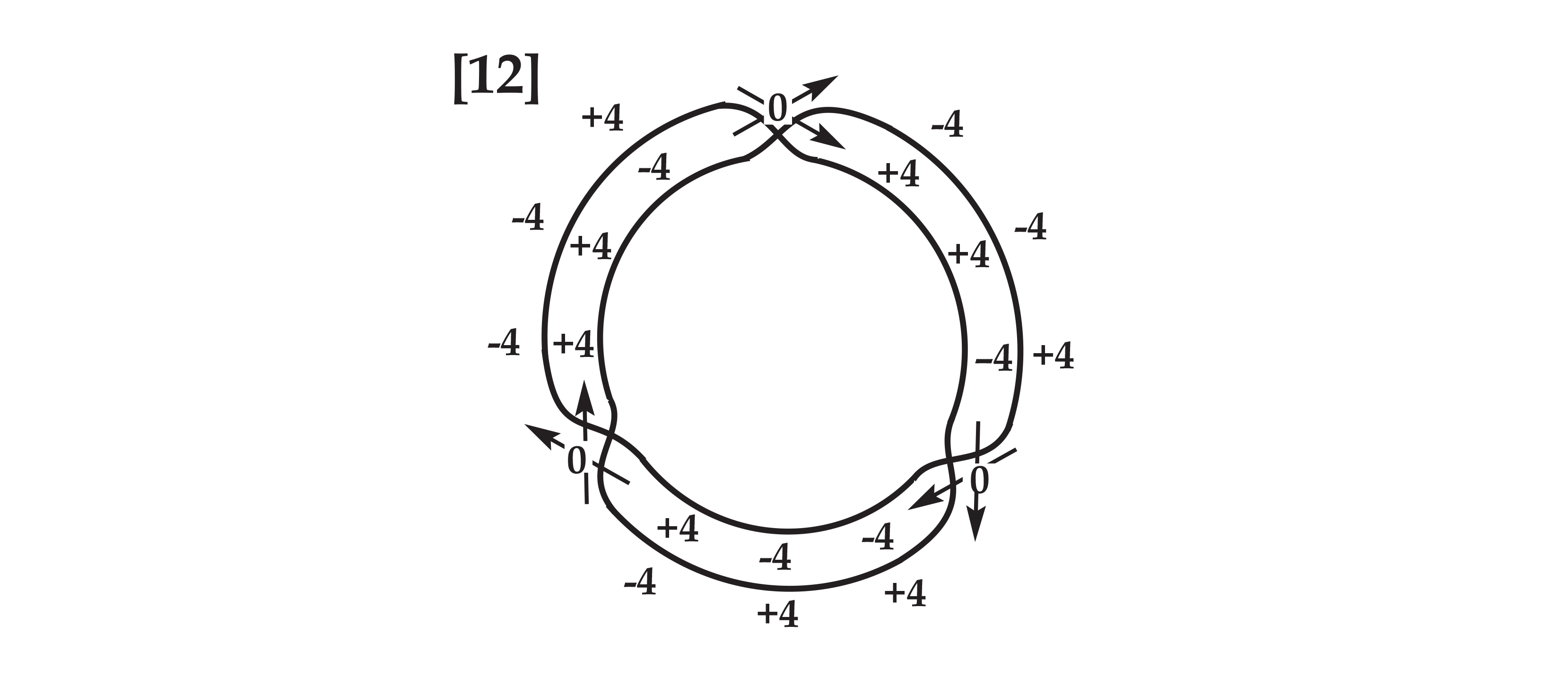
Subtracting a sequence from itself at a distance of twelve indexical degrees, that is, subtracting unitary counterparts, we can see that their difference turns out to be modulated by the ternary sequence:

Finally, the quaternary non-linear sequences govern transposition by minor thirds, allowing a sort of major/minor translation

Non-Linear Arborescences

We have already noted that a directed minimum curve is a minimum hierarchical constituency, in that the one interval encompasses the other two. We can elaborate this hierarchy arbitrarily by inserting an intervening pitch between the initial pitch and its destination, bisecting each sub-interval into a new curve. We can continue bisecting the sub-intervals that result from this bisection in the same manner. When applied in this way, proportional categories form an adequate basis for all further elaboration of heirarchical (compositional) structure.

We can construct a linear intervallic heirarchy by taking one of the linear elements from the harmolodic matrix, and interpolating a new pitch after each existing pitch using a single intervallic function. We arrive at a familiar pattern:

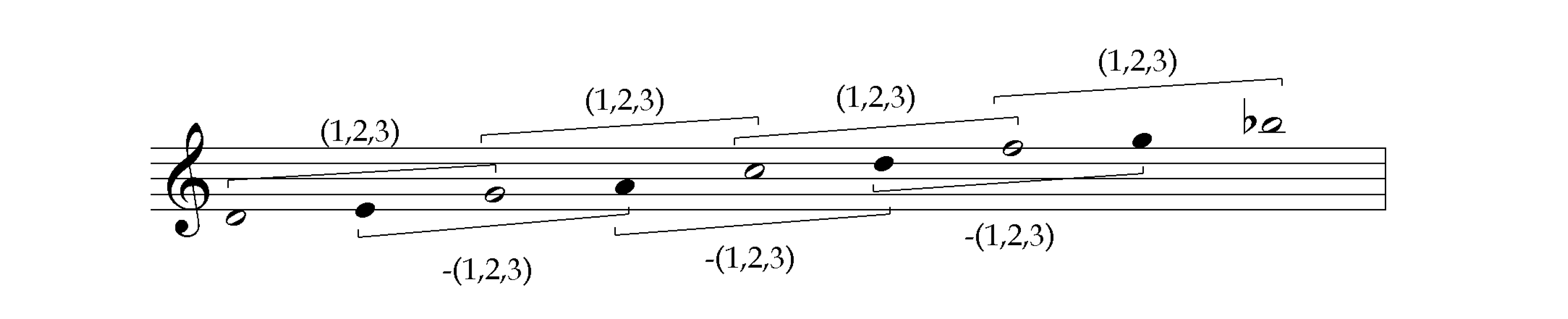
This rudimentary arborescence is simply the linear elaboration of a proportion; we have already used it to illustrate co-derivative proportional categories. The proportion is repeatedly modulated by one of its three constituent intervals, with each iteration framing the other two intervals. As we have noted, the notes interpolated within each frame are themselves generated by the same intervallic function, and frame inversions of the proportion. In general, linear arborescences elaborate a trajectory along one of the linear axes of the harmolodic matrix by inserting nested deviations along other axes.

We can now derive a class of infinitely detailed arborescences that display non-linear curvature on every order of difference and every scale of magnitude. They will allow us to elaborate these hyperdynamic modulatory sequences to an arbitrary degree of precision and detail, completing a harmolodic toolkit that allows a composer to mix harmonic inertia and harmonic acceleration freely.

As noted above, the operation that derives directed minimum curves from intervals is analogous to the operation that derives arborescences from interval sequences. So we need a principle for determining a latent third pitch that resides between any two consecutive pitchs, and splits each interval into two intervals, inserting a minimum curve at higher degree of resolution.

Non-linear sequences are constructed by reiterating the total interval of the last minimum curve – the sum of the last two intervals – in a single jump. Thus it is clear that an intermediate pitch for each interval in these sequences is covertly specified in the preceding trichord. Each interval arose in the first place as an abbreviation of the preceding two intervals, so it is merely a matter of reinserting the pitch that was elided when the overall interval that framed it was duplicated.

The duplication of this intermediate pitch introduces a redundancy, thereby depriving us of our goal of total curvature. This redundancy becomes more pervasive with every bisection. After two iterations—that is, after we bisect each interval in a non-linear interval sequence to match the preceding minimum curve, then bisect each of the new intervals similarly—the emergent linearity is already striking:

With each bisection, this arborescence reintroduces a greater degree of linearity to the non-linear sequence it elaborates. In a way it effects the converse of linear arborescences: just as the latter introduce local curvature in a global linearity by interpellating one constant within another, the above bisections effectively introduce local linearity in a global curvature by echoing each interval class.

It would appear that in order to prevent linearity from seeping into these arborescences we will have to associate the intervals in the original interval sequences with ordered trichords which are not adjacent to them; as long as the framing interval of an ordered trichord is associated with the interval that immediately follows it, we will not be able to reinsert the intermediate pitch into the latter without introducing redundancy.

And in fact, our non-linear sequences do associate non-adjacent positions. For as we noted earlier, these sequences intersect themselves such that every interval class has a twin elsewhere in the same sequence:

Thus, each interval class can be bisected into the two interval classes that precede its twin. Each of these interval classes can be similarly bisected, ad infinitum:

Each indexical position thereby branches into infinitely detailed non-linear curve which can be articulated to any degree of resolution. Each of these perfectly smooth and dynamic curves is associated with a specific minimum curve: the one created by the first bisection of the indexical position in question. Conversely, each minimum curve is elaborated recursively with the inventory of 24 curves that correspond to the indexical positions of the original non-linear sequence. As with the original non-linear sequence, no one curve is necessarily heirarchically prior to the others; each position subdivides into all the others through a series of bisections.

These curves form an abelian group which is homologous that of the foundational non-linear sequences. So, for instance, if two curves belonging to adjacent indexical positions were superimposed, the resultant vertical intervals would form another twelve-fold curve. But if an A and a D curve belonging to the same indexical position were superimposed, the resultant vertical intervals would be only unisons and tritones—a binary curve.

Each bisection splits one interval into two. Repeated bisection of antecedent or consequent interval classes reveals left-branching and rightbranching pedigrees which return to a given curve every 3, 6, or 12 generations. For instance, D5 is a part of the following left-branching pedigree:

The four direct arborescences each contain 5 antecedent pedigrees of 3 or 6 generations each, and 2 consequent pedigrees of 12 generations each. The retrograde arborescences have the exact same pedigrees in reversed positions, as each pitch in the original non-linear sequence is effectively attached to the pitches which precede it in the direct forms. If we label the antecedent pedigrees A through E and the consequent pedigrees Y and Z, they correspond to the indexical positions of the direct arborescences in the following pattern:

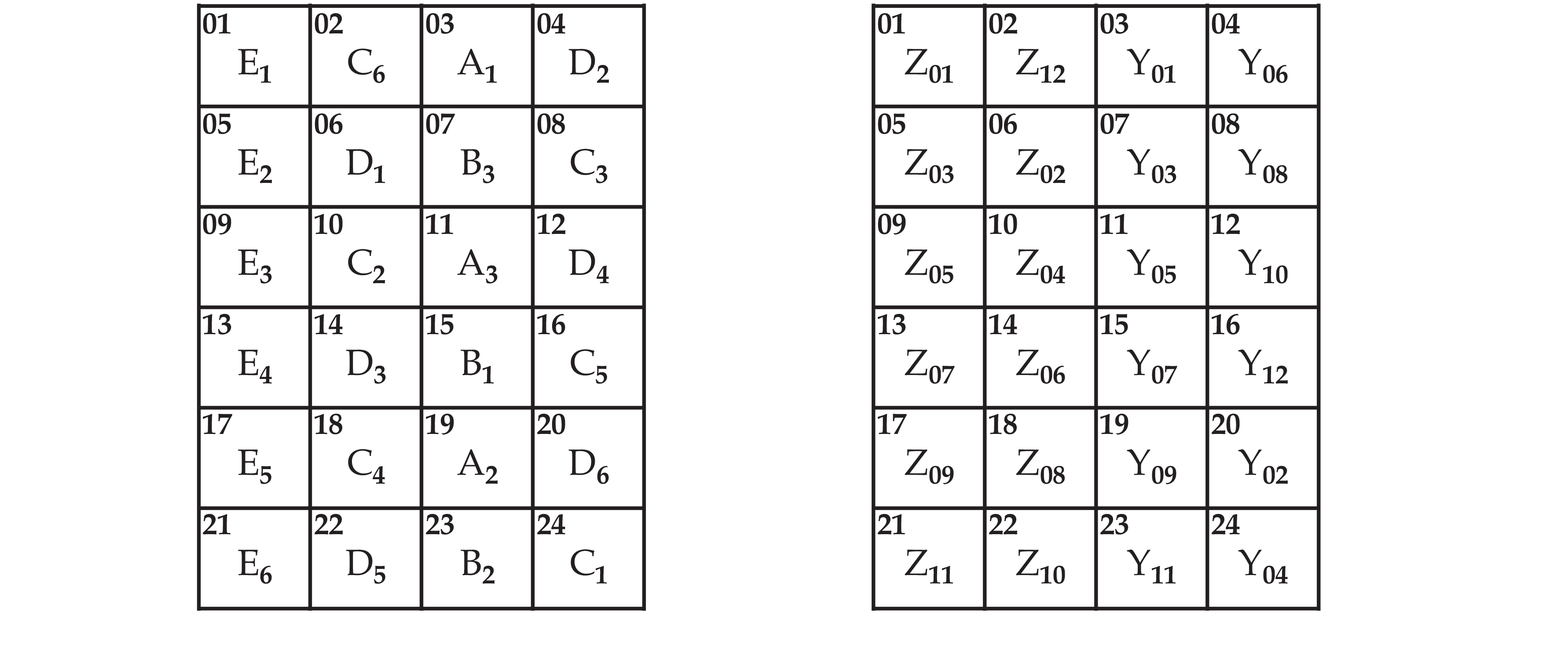
The sequence of antecedent pedigrees repeats every eight positions, just as the ternary non-linear sequence repeats every eight values; both articulate the unitary non-linear sequences in a ternary translational symmetry. As we noted above, interval by the ternary sequence can effect substitution of unitary counterparts, that, is mutual substitution of gradient and harmonic units.

The antecedent pedigrees correspond to specific positions in this sequence of |4| interval that effects unitary substitution. Here are the antecedent pedigrees as viewed on the moebius strip of unitary duals:

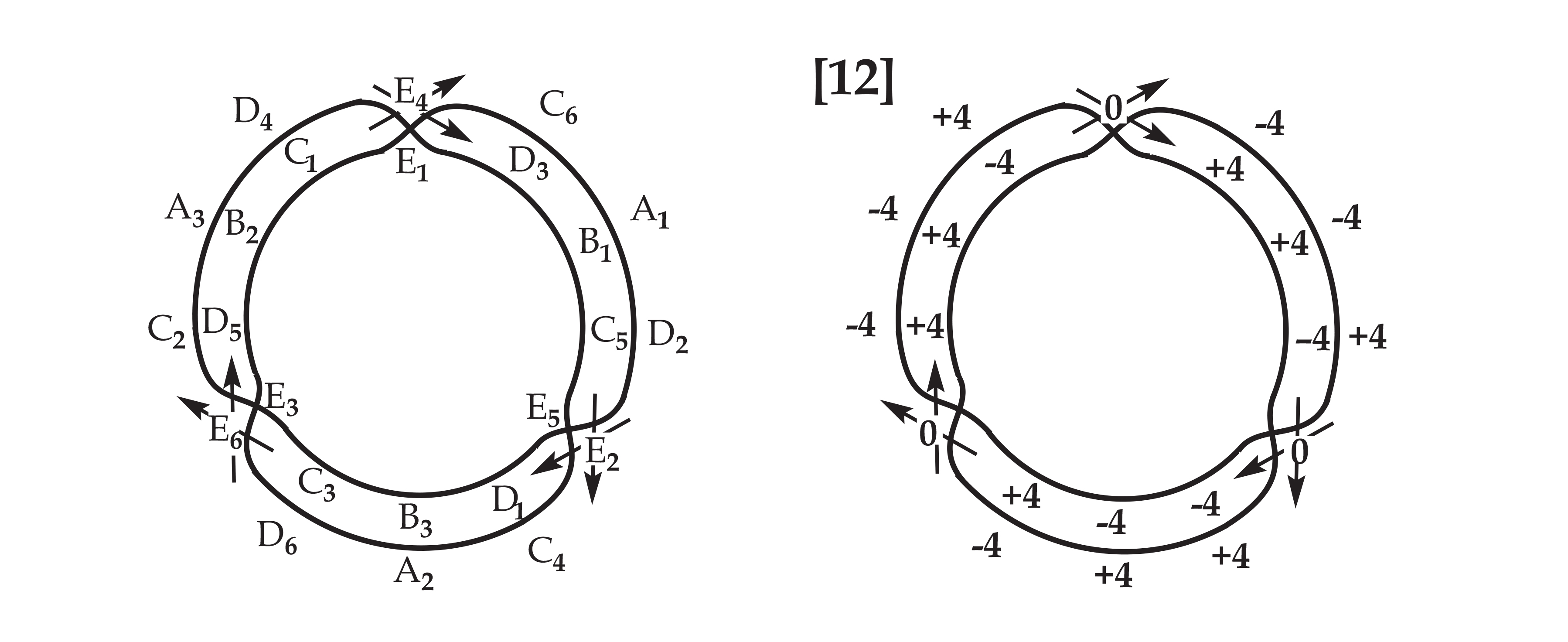
Just as the substitution of gradient units (half-steps) for harmonic units (fifths) in the non-linear sequences results in the very same sequences shifted by twelve indexical positions, unitary substitution within one of these non-linear curves produces the curve located twelve indexical positions away. Among the antecedent pedigrees, the A pedigrees and C pedigrees correspond to +4 transposition, the B pedigrees and the D pedigrees correspond to -4 transposition, and the E pedigrees correspond to null transposition. Unitary substitution corresponds to an interval by a distinct ternary curve for each of these three positions.

• References
• Ornette: Made in America. Directed by Shirley Clarke. 1985. Film.
• Edmondson, Amy C. A Fuller Explanation: The Synergetic Geometry of R. Buckminster Fuller. Boston: Birkhäuser, 1987.
• Fuller, R. Buckminster, and E. J. Applewhite. Synergetics: Explorations in the Geometry of Thinking. New York: Macmillan, 1975.
• Mathieu, W. A. Harmonic Experience: Tonal Harmony from Its Natural Origins to Its Modern Expression. Rochester, Vt.: Inner Traditions International, 1997.
• O’Connell, Walter. “Tone Spaces.”Die Reihe 8 (English ed. 1968): 35-67.
• Pinter, Charles C. A Book of Abstract Algebra. 2nd ed. New York: McGraw-Hill, 1990.
• Snaith, Victor P. Groups, Rings and Galois Theory. Singapore: World Scientific, 1998.